表面活性劑的自組裝行為
表面活性劑是一類兩親分子,包含親水基和親油基兩部分.當表面活性劑在水溶液中時,親油基團總是傾向於脫離極性的水環境,於是在低濃度情況下,表面活性劑就能自發地吸附在氣液界面,形成定向單分子層。當表面活性劑的濃度繼續增加,界面吸附達到飽和時,表面活性劑的親油基為了儘可能的脫離水環境,就會自發的在水溶液中形成親水基向水,親油基處於內部的聚集體,這一過程稱為自組裝。
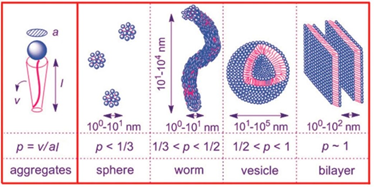
正是由於表面活性劑分子中同時存在親水基和親油基,使其能在不同的水溶液中自組裝形成球形、蠕蟲狀、囊泡等多種膠束結構。為了更好的解釋表面活性劑在水溶液中的不同聚集行為,Israelachivili等提出了“堆積參數”理論.其堆積參數P的公式為:
P=v/al
 表面活性劑的自組裝行為
表面活性劑的自組裝行為式中v和l分別表示疏水鏈的最大有效體積和長度,a為構成聚集體的每個表面活性劑分子在表面活性劑/水界面上所占的有效面積.當P小於1/3時,聚集體易為球形膠束;當1/3<P<1/2時,易形成蠕蟲狀膠束;當1/2<P<1,可形成囊泡結構;而當P在1左右時,聚集體有可能為層狀結構。
表面活性劑分子的結構很大程度上決定了堆積參數P的值。通常單疏水鏈的表面活性劑分子的堆積參數P<1/2,在水溶液中易形成球形膠束,而當表面活性劑分子中含有兩條疏水鏈的時候,堆積參數P通常在1/2和1之間,這時在水溶液中有較大可能形成囊泡結構.除此之外,表面活性劑分子的自組裝結構還與表面活性劑自身的濃度和外界環境有關。這些外界環境包括溫度、pH和鹽度等。
蠕蟲狀膠束的外觀特徵
蠕蟲狀膠束具有黏彈性特徵。所謂的黏彈性,是指其具有液體的黏性特徵同時也具有固體的彈性特徵。通常,蠕蟲狀膠束的黏彈性較好時,可以倒立在小瓶子中,而不流動。總之,蠕蟲狀膠束最主要的特徵是其黏彈性,從肉眼上可以看出蠕蟲狀膠束體系的流動性差並且具有一定的彈性。
 蠕蟲狀膠束的外觀照片
蠕蟲狀膠束的外觀照片蠕蟲狀膠束的流變性為簡介
流體的類型
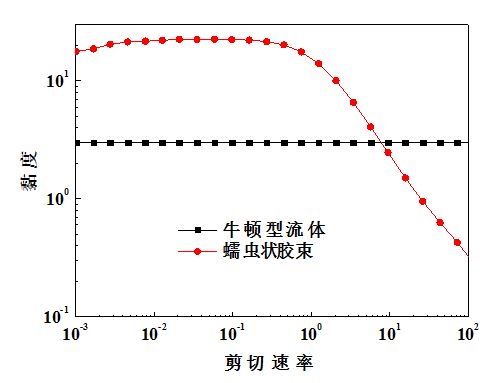
根據流體流變曲線的不同可以將流體分為牛頓型流體和非牛頓型流體.牛頓型流體是指流體的流變曲線中的剪下應力σ和剪下速率γ成線性關係,即符合牛頓黏性定律.其公式為:
式中η為黏度.不符合牛頓黏性定律的流體則為非牛頓型流體.牛頓型流體的黏度只與溫度有關,不隨剪下應力的變化而變化,即剪下應力與剪下速率成正比關係。
在穩態流變圖上,蠕蟲狀膠束所構成的流體在低剪下速率時,體系的黏度不隨剪下應力的變化而變化,即符合牛頓型流體的特點,此時體系的黏度稱為零剪下黏度η0,是反應蠕蟲狀膠束黏度大小的一個重要物理量;當剪下速率超過一定值時,蠕蟲狀膠束的黏度開始下降,即存在剪下稀釋現象。根據這一特點可用來判斷蠕蟲狀膠束的存在。
 蠕蟲狀膠束和牛頓型流體的對比
蠕蟲狀膠束和牛頓型流體的對比Maxwell流體模型
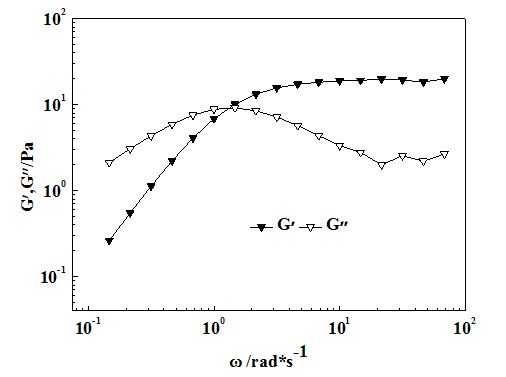
蠕蟲狀膠束的流體行為符合Maxwell流體模型[[i],其具體關係可用下列關係式表示:
(公式2)
tR = 1/ωc
式中
G'為彈性模量,又稱為儲能模量,反應蠕蟲狀膠束的彈性大小;
G''為黏性模量,又稱為損耗模量,反應蠕蟲狀膠束的黏度大小;
G0是平台模量,其值為體系在高頻率時彈性模量
G'的平台值,反應蠕蟲狀膠束纏繞點的密度大小;
ω為振盪角頻率;
ωc為彈性模量
G'和黏性模量
G''交點所對應的振盪角頻率
ω值;
tR為弛豫時間,反應蠕蟲狀膠束的平均長度。
對於蠕蟲狀膠束來說,在低振盪角頻率處,其彈性模量G'大於黏性模量G'',體系主要表現彈性行為;在高振盪角頻率處,其黏性模量G''大於彈性模量G',體系主要表現黏性行為。在動態流變圖上通常可以看到一個交點。
 蠕蟲狀膠束的動態流變圖
蠕蟲狀膠束的動態流變圖Cole-Cole 規則是檢驗蠕蟲狀膠束是否符合Maxwell流體模型的一種簡單有效的方法。將公式(1)和公式(2)聯立可得下列公式:
對G'- G''作圖,G'- G''圖應呈半圓形,該半圓的直徑應為G0,該圖稱為Cole-Cole圖。
 蠕蟲狀膠束的Cole-Cole圖
蠕蟲狀膠束的Cole-Cole圖 表面活性劑的自組裝行為
表面活性劑的自組裝行為 蠕蟲狀膠束的外觀照片
蠕蟲狀膠束的外觀照片 蠕蟲狀膠束和牛頓型流體的對比
蠕蟲狀膠束和牛頓型流體的對比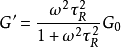

 蠕蟲狀膠束的動態流變圖
蠕蟲狀膠束的動態流變圖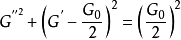
 蠕蟲狀膠束的Cole-Cole圖
蠕蟲狀膠束的Cole-Cole圖
