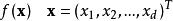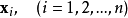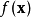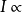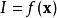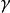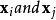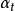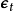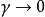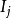螢火蟲算法

螢火蟲算法（Firefly Algorithm）是一種啟發式算法，靈感來自於螢火蟲閃爍的行為。螢火蟲的閃光，其主要目的是作為一個信號系統，以吸引其他的螢火蟲。劍橋大學的Xin-She Yang（音譯：楊新社）教授提出了螢火蟲算法，其假設為：

螢火蟲不分性別，這樣一個螢火蟲將會吸引到所有其他的螢火蟲;吸引力與它們的亮度成正比，對於任何兩個螢火蟲，不那么明亮的螢火蟲被吸引，因此移動到更亮的一個，然而，亮度又隨著其距離的增加而減少;如果沒有比一個給定的螢火蟲更亮的螢火蟲，它會隨機移動。

亮度應與目標函式聯繫起來。螢火蟲算法是以自然為靈感的啟發式最佳化算法。

基本介紹

• 中文名：螢火蟲算法
• 外文名：Firefly Algorithm
• 類別：仿生群智慧型最佳化算法
• 提出者：Xin-She Yang
• 靈感來源：來自於螢火蟲閃爍的行為
• 學科：光學

算法描述

螢火蟲算法的偽代碼可以概括為：

Begin

1）目標函式

2）生成一個螢火蟲的初始入口

3）制定光照強度l，因此，它與 （例如，對於最大化問題或;

4）定義吸收係數

while(T < MaxGeneration)

for i =1:n(所有n螢火蟲)

for j =1:n(n螢火蟲)

if({\displaystyle I_{j}>I_{i}})，

移動螢火蟲i向j;

end if

吸引力與距離;

評估新的解決方案和更新的光強度;

end for j

end for i

排名螢火蟲和找到當前最佳;

end while

處理後的結果和可視化;

end

對於任何一兩隻螢火蟲的主要更新公式是，其中是步長參數, e 是一個矢量（服從高斯或其他的分布）。

可以證明在的情況，FA可以簡化為 準粒子群最佳化(PSO).事實上，，如果內環（j）條被刪除，亮度 替換為當前的全球最佳，FA基本上成為標準PSO。

螢火蟲算法的變種

離散螢火蟲算法

離散形式的螢火蟲算法（Discrete Firefly Algorithm，DFA）DFA優於現有算法如蟻群算法。

對於圖像分割，基於FA-方法比Otsu的方法更為有效.同時， 離散螢火蟲算法對QAP問題，Durkota已進很好的實現行

針對負荷預測中的特徵選擇問題，套用FA實現Wrapper特徵選擇算法.

多目標螢火蟲算法

Apostolopoulos and Vlachos對FA進行了一個重要的多目標研究。同時，Yang提出了多目標螢火蟲算法（Multiobjective Firefly Algorithm，MOFA），對連續最佳化問題有很好的效果。

拉格朗日FA

拉格朗日螢火蟲算法用來解決電力系統最佳化單元承諾問題。

混沌FA

混沌螢火蟲算法（Chaotic Firefly Algorithm，CFA）也顯示了算法的有效性。

混合算法

螢火蟲算法與蟻群最佳化算法相結合的混合算法，能夠解決金融投資組合最佳化。

Memetic 算法

一種基於螢火蟲算法（FA）的Memetic算法（FA-MA）被用來最佳化支持向量機（SVR）預測模型的參數。在該FA-MA中，FA用來搜尋全局解空間，而模式搜尋（pattern Search） 被用來進行個體學習和局部解空間搜尋。

實際套用

螢火蟲算法已被套用到幾乎所有領域科學和工程，如數字圖像壓縮和圖像處理,特徵值最佳化,特徵提取和故障檢測,天線設計,工程結構設計, 調度和旅行商問題,語義組成,化學相平衡， 聚類,動態問題, 剛性圖像配準問題,參數選擇，蛋白質摺疊問題等等。