過半徑為a的定圓上一個定點O,任作一直線l交圓周於另一點P0,在l上取P點,使得|PP0l=b(b>0),則P點的軌跡稱為蝸線,也稱為蚶線。
基本介紹
- 中文名:蚶線
- 外文名:limacon (of Pascal);Pascal’s snail
- 所屬學科:數學(幾何學)
- 相關概念:蚌線(或螺形線)
- 別稱:蝸線、帕斯卡蚶線
定義,蚶線的形狀,蚶線的方程,蚶線的基本性質,
定義
設C是一條已知曲線,O是一個定點,通過O作直線和曲線C相交於點P,在這直線上點P的兩側各取一點M,使|PM|總等於某個定長 ,那么,這種點M的軌跡叫作已知曲線C關於已知點O的蚌線(或螺形線)。曲線C叫作蚌線的基線,定點O叫作蚌線的極點,定長
,那么,這種點M的軌跡叫作已知曲線C關於已知點O的蚌線(或螺形線)。曲線C叫作蚌線的基線,定點O叫作蚌線的極點,定長 叫作蚌線的間隔。
叫作蚌線的間隔。


設C是平面上的一個定圓,O是位於定圓C上的一個定點,那么,圓C關於點O的蚌線叫作帕斯卡蚶線(或蝸線),簡稱蚶線。
蚶線的形狀
由蚶線的定義,不難描繪出蚶線,由於定圓C的直徑h與間隔a的大小關係不同,蚶線呈現三種不同的形狀,如表1。當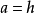 時,這種特殊的蚶線也叫作心臟線。
時,這種特殊的蚶線也叫作心臟線。
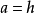
  | 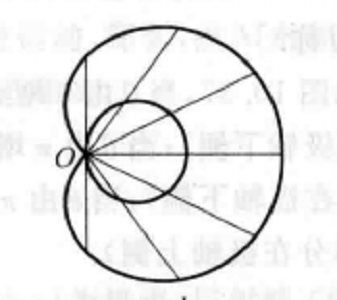  | 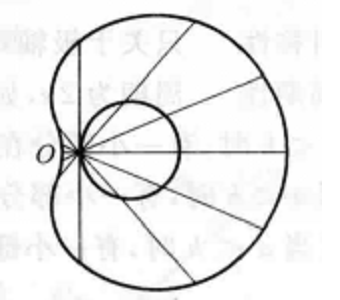 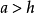 |
蚶線的方程
如圖2,以蚶線的極點 為端點,通過基線圓的圓心作射線
為端點,通過基線圓的圓心作射線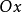 ,以點
,以點 為極點,以
為極點,以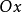 為極軸建立極坐標系,設基線圓的直徑為h,蚶線的間隔為
為極軸建立極坐標系,設基線圓的直徑為h,蚶線的間隔為 ,蚶線上任意一點M的極坐標為
,蚶線上任意一點M的極坐標為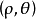 ,那么,
,那么, 。由於
。由於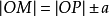 ,所以有
,所以有

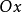

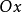

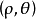

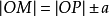

 圖2
圖2和蚌線的情形一樣
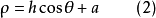
和

定理1以蚶線的極點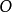 為極點,以通過基線圓的圓心的射線
為極點,以通過基線圓的圓心的射線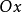 為極軸建立坐標系,若蚶線的基線圓的直徑為h,間隔為
為極軸建立坐標系,若蚶線的基線圓的直徑為h,間隔為 ,則這蚶線的極坐標方程為
,則這蚶線的極坐標方程為
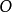
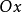

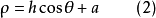
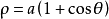
蚶線的基本性質
蚶線(2)的基本性質:
(1)對稱性 只關於極軸對稱。
(2)周期性 周期為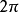 ,如表2,當
,如表2,當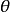 由0增大到
由0增大到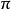 時,得到蚶線的上半部(當
時,得到蚶線的上半部(當 時,有一小部分在極軸下側);當
時,有一小部分在極軸下側);當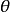 由
由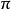 增大到
增大到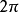 時,得到蚶線的下半部(當
時,得到蚶線的下半部(當 時,有一小部分在極軸下側);當
時,有一小部分在極軸下側);當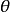 由
由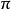 增大到
增大到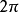 時,得到蚶線的下半部(當
時,得到蚶線的下半部(當 時,有一小部分在極軸上側)。
時,有一小部分在極軸上側)。
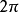
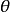
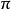

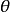
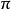
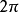

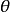
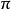
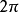

(3)存在範圍 因 ,所以
,所以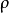 不能無限增大,所以蚶線囿於一有限範圍內。
不能無限增大,所以蚶線囿於一有限範圍內。