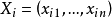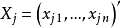基本介紹
- 中文名：蘭氏距離
- 外文名：Canberra
- 所屬學科：數學
- 所屬問題：統計學（多元分析）
基本介紹,相關概念,
基本介紹
在聚類分析過程中，需要區分為不同的類，事物是怎樣劃分到不同的類別當中的呢?判斷不同事物是否歸於一類依據的是事物之間的相似性。事物相似性的度量標準一般有兩種：距離和相似性係數，距離一般用來度量樣本之問的相似性，而相似性係數。一般用來度量變數之間的相似性。
距離是將一個樣本看做M維空間中的一個點，並在空間中定義距離，距離較近的點可以歸入同一類，距離遠的點歸入不同的類。
聚類分析中的距離一般用來測驗樣本之間的相似性，是進行聚類分析的關鍵步驟。當分析數據的類型為非連續性數據，則需要使用卡方分析方法來計算其距離；而當分析數據的類型為連續性數據時，則可以使用明氏、馬氏、蘭氏距離，或自定義距離方法來計算其距離。
蘭氏距離是一個無量綱的量，克服了閔可夫斯基距離與各指標的量綱有關的缺點，且蘭氏距離對大的奇異值不敏感，這使其特別適合高度偏移的和數據。但蘭氏距離也沒有考慮變數間的相關性。
閔可夫斯基距離和蘭氏距離都是假定變數之間相互獨立，即在正交空間中討論距離。但在實際問題中，變數之間往往存在著一定的相關性，為克服變數之間相關性的影響，可以採用馬氏距離。
蘭氏距離定義為
相關概念
(1)絕對值距離
絕對值距離，也稱為曼哈頓距離，計算方法如下：
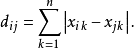
(2)歐氏距離
歐氏距離，也稱為L2範數，計算方法如下：
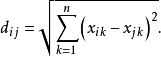
(3)切比雪夫距離
切比雪夫距離，計算方法如下：
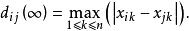
(4)明考夫斯基距離
明考夫斯基距離不是單一一個距離，而是一組距離的定義，計算方法：
明考夫斯基距離以及切比雪夫距離存在以下兩個缺點：
①明考夫斯基距離的值與各指標的量綱有關，明考夫斯基距離對各指標計量單位差異在計算距離時沒有任何區分。例如，2維特徵(成績，年齡)，3個樣本(70，18)，(90，19)，(80，18)之間的距離很難用數值表達。
②明考夫斯基距離的定義沒有考慮多維向量各變數之間的相關性和分布差異。明考夫斯基距離把各個變數都同等看待，將兩個樣本在各個變數上的離差簡單地進行了綜合。
(5)標準化歐氏距離
標準化歐氏距離是針對簡單歐氏距離的缺點而作的一種改進方案。標準歐氏距離將各個分量用均值和標準差標準化，標準化後的變數去除了變數分布差異，計算方法為
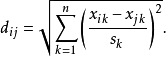
(6)馬氏距離
馬氏距離是印度著名統計學家馬哈拉諾比斯(P.C.Mahalanobis)所定義的一種距離，其計算公式為
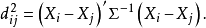
Xi和Xj分別表示第i個樣本和第j個樣本的觀測值所組成的列向量，即：樣本數據矩陣中第i個和第j個行向量的轉置，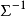
表示觀測變數之間的協方差矩陣。在實踐套用中，若總體協方差矩陣未知，則可用樣本協方差矩陣作為估計代替計算。若協方差矩陣是單位矩陣(各個樣本向量之間獨立同分布)，則公式為
