薄膜比擬是實驗應力分析中常用的一種比擬方法。利用彈性薄膜同扭轉和彎曲問題的相似性,通過對薄膜的研究來確定扭轉和彎曲問題中的未知量。
基本介紹
- 中文名:薄膜比擬
- 外文名:membraneanalogy
歷史,原理,套用,扭轉,彎曲,
歷史
德國的L.普朗特在固體力學方面有不少貢獻。他的博士論文(1899)探討了狹長矩形截面梁的側向穩定性。1903年提出了柱體扭轉問題的薄膜比擬法,後來被A.A.格里菲思和G.I.泰勒用來確定各種複雜截面形狀柱體的抗扭剛度。
原理
從彈性理論得知,均勻張緊的彈性薄膜的橫向撓曲和等截面受扭直桿的橫截面中的剪應力,都由泊松方程描述:


其邊界條件分別為:


式中w為薄膜的撓度;p為單位面積上的橫向力; 為薄膜邊界上單位長度內的拉力;ψ為扭轉應力函式;G為剪下模量;θ為單位長度的扭轉角(弧度);Si為薄膜和桿件的橫截面的邊界(i=1,2);x、y為直角坐標。由此可見,如薄膜的邊界在一個水平面上,其形狀和受扭桿件的橫截面相似,而且Cp/
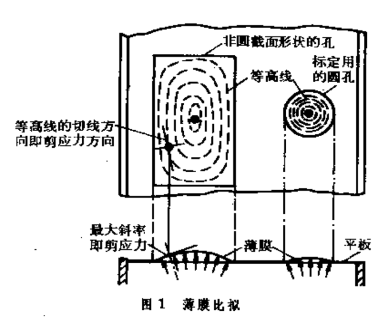
為薄膜邊界上單位長度內的拉力;ψ為扭轉應力函式;G為剪下模量;θ為單位長度的扭轉角(弧度);Si為薄膜和桿件的橫截面的邊界(i=1,2);x、y為直角坐標。由此可見,如薄膜的邊界在一個水平面上,其形狀和受扭桿件的橫截面相似,而且Cp/ =2Gθ (C為比例常數),則撓度w(x,y)和扭轉應力函式ψ(x,y)成比例。試驗時,在一塊平板上開一個和受扭桿件的橫截面形狀相似的孔,將薄膜(如橡皮膜、肥皂膜等)張在孔上,然後在薄膜的一側微微施加氣壓,使它撓曲。測繪出薄膜撓曲後的等高線(圖1)。由等高線圖可得出如下結果:①薄膜上任意點的等高線的切線方向,就是受扭桿件橫截面上的對應點的剪應力方向。②薄膜上任意點的最大斜率(可由等高線的豎直和水平間距算出)和受扭桿件橫截面上對應點的剪應力大小成比例。若在同一平板上開一圓孔(如圖1右邊的圓孔),張上相同的薄膜,並施加同樣的氣壓,就可以標定出這一比例值。③撓曲薄膜表面和平板表面之間所包含的體積和受扭桿件的扭矩成比例。
=2Gθ (C為比例常數),則撓度w(x,y)和扭轉應力函式ψ(x,y)成比例。試驗時,在一塊平板上開一個和受扭桿件的橫截面形狀相似的孔,將薄膜(如橡皮膜、肥皂膜等)張在孔上,然後在薄膜的一側微微施加氣壓,使它撓曲。測繪出薄膜撓曲後的等高線(圖1)。由等高線圖可得出如下結果:①薄膜上任意點的等高線的切線方向,就是受扭桿件橫截面上的對應點的剪應力方向。②薄膜上任意點的最大斜率(可由等高線的豎直和水平間距算出)和受扭桿件橫截面上對應點的剪應力大小成比例。若在同一平板上開一圓孔(如圖1右邊的圓孔),張上相同的薄膜,並施加同樣的氣壓,就可以標定出這一比例值。③撓曲薄膜表面和平板表面之間所包含的體積和受扭桿件的扭矩成比例。


如果薄膜上的單位面積的橫向力p=0,則可模擬拉普拉斯方程描述的力學問題,即


在平面應力場中,ψ=(σ1+σ2)表示主應力和,它和薄膜的高度h成比例。薄膜比擬特別適用於確定非圓截面桿件的扭轉性能。
套用
扭轉
研究承受均勻橫向壓力作用的彈性薄膜的變形問題可以發現,當薄膜中的某呰物理量(如壓力和表面張力)和柱體扭轉問題中的某些物理量(如單位長度的扭轉角θ和剪下模量G)之間滿足一定的關係時,扭轉問題中的物理量的數值可由和柱體截面形狀相同的薄膜中相應的物理量的數值來確定。例如,柱體中任意一點剪應力分量可由薄膜對應點處與剪應力垂直的方向上薄膜的斜率來確定。由此可以得出結論:剪應力合力的方向是薄膜等高線的切線方向,最大剪應力出現在薄膜等高線最稠密的點。
在略去局部應力的影響後,用薄膜比擬法求得的狹矩形截面柱體的扭轉結果可用於求解開口薄壁桿件的扭轉。若用薄膜比擬法求解具有兩個或兩個以上邊界的薄壁桿件的扭轉問題,則需要將內邊界用無重量的剛性平板來代替,並利用薄膜罩住的體積的兩倍等於扭矩的關係以及剪應力環量公式聯立求解,這樣便可得到剪應力分量。所謂剪應力環量公式就是剪應力在薄膜等高線上的積分為常數,即

式中A為等高線所包圍的面積。
彎曲
懸臂柱體的彎曲問題可同僅受均勻拉力作用的薄膜進行比擬。比擬時應將薄膜張緊在一個和柱體截面形狀相同的水平孔上,薄膜的高度即為截面上相應點的應力函式,將得到的代入下式便可得到剪應力分量: