莫里三角形

莫里三角形，是紀念它的發現者英國數學家弗蘭克·莫里。莫里在1899年發現了這個三角形。如左圖的紅色三角形，就是莫里三角形。莫里三角形總是一個正三角形。

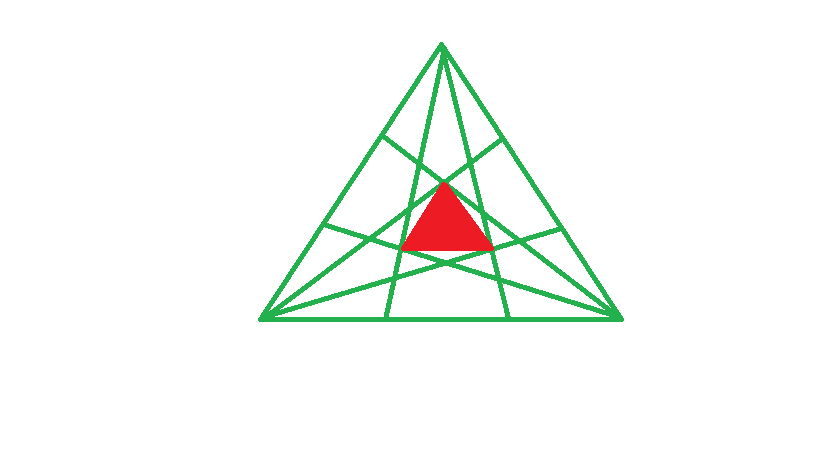
基本介紹

• 中文名：莫里三角形
• 外文名：Murray triangle
• 別稱：莫利三角形，內莫利三角形
• 表達式：無
• 提出者：弗蘭克·莫里
• 提出時間：1899年
• 套用學科：數學
• 適用領域範圍：平面幾何

方法

一、畫一個三角形。

二、將這個三角形的三條邊進行三等分。

三、連線三角形頂點與對應邊上的三等分點。

四、得出圖形為一個六邊形。

五、將這個六邊形的上、左下和右下三點連線，得出的三角形就是一個正三角形，這個正三角形又被稱作莫里三角形。

證明

畫出最中間的三角形，也就是莫里三角形後，求證：是否任意一個三角形經過這樣的步驟以後，最中間的三角形都是一個正三角形呢？

證：要證明這個問題很簡單，

因為只要是軸對稱的凸六邊形，

上、左下、右下或者下、左上、右上這兩種方法圍出的三角形，

一定是正三角形。

那么求證可轉化：

是否任意一個三角形經過這樣的步驟以後，

可以圍成一個軸對稱的凸六邊形呢？

由於經過這樣的步驟以後，

每一條直線就是六邊形的一條邊，

又因如果六條直線經過穿插而成的有六邊形和六個小三角形，

六邊形不可能不對稱，也不可能為凹形，

所以任意一個三角形經過這樣的步驟以後，最中間的三角形都是一個正三角形。