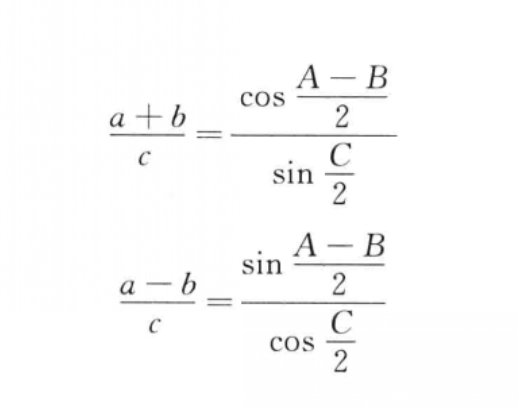莫爾韋德公式(Mollweide's formula)是關於三角形邊角關係的一組公式。此公式每個都含有三角形的六個基本元素,常用它們作解三角形的驗算,該公式由莫爾韋德(K.B.Mollweide)於1808年發表在他的著作中,故以此得名。其實,牛頓(I.Newton)早在1707年發表的《通用算術》中,已給出其中的一個公式,隨後,馮·奧佩爾(Von Oppel)的《解析三角學》與辛普森(T.Simpson)的《三角》中都早有此公式。
基本介紹
- 中文名:莫爾韋德公式
- 外文名:Mollweide's formula
- 所屬學科:數學
- 所屬問題:平面幾何(三角學)
- 相關人物:莫爾韋德、牛頓、馮·奧佩爾
- 簡介:關於三角形邊角關係的一組公式
基本介紹,公式證明,
基本介紹
下面的兩個比例式叫作莫爾韋德公式,一個含有三角形的二邊之和與其第三邊的比,另一個含有三角形的二邊之差與其第三邊的比


僅就平面三角形說,在莫爾韋德(1774-1825)以前,奧貝爾(F.W.Oppel)於1746年已給出這兩個公式;其中的第一個,牛頓(1 642-1727)也先知道了,辛普森(T.Simpson 1710-1761)所著的三角學課本中已載有兩個公式的完善證明。
公式證明
輔助定理
三角形的任一邊,等於外接圓的直徑與此邊所對之頂角的正弦之積。
用R表示外接圓的半徑,則所需證明的是:a=2R·sin A,此處∠A可為銳角亦可為鈍角。
證明: 1)∠A為銳角(圖1),在外接圓里,由已知邊之一端引直徑,將此
邊之他端連線起來,得一直角三角形,在圖1里此三角形為BDC:易得:BC=BD·sin D或a=2R·sin D,但∠D=∠A;所以a=2R·sin A。
2)∠A為鈍角,仍按1)的方法,作輔助圖形。則由直角三角形BCE(圖2)知:a=2R·sin E;但∠E+∠A=180,故sin E=sin A,由此得:a=2R·sinA。
故可得出一般的公式
a=2R·sin A,b=2R·sin B,c=2R·sin C.
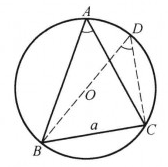
圖1
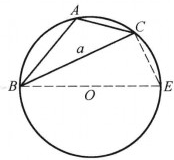
圖2
莫爾韋德公式的證明
證明 (1)由輔助定理得







2)同樣可得