茹利亞方向(Julia direction)是指函式值分布的奇異方向。對於超越整函式(或超越亞純函式),茹利亞方向是複平面C內由原點出發的具有下述性質的半射線J={z|arg z=θ0}。
茹利亞(Julia,G.M.)於1919—1921年套用蒙泰爾(Montel,P.A.)創立的正規族理論證明,任一超越整函式至少存在一條茹利亞方向。
基本介紹
- 中文名:茹利亞方向
- 外文名:Julia direction
- 領域:數學
- 定義:函式值分布的奇異方向
- 對象:超越整函式或超越亞純函式
- 人物:茹利亞、蒙泰爾
概念,整函式,亞純函式,人物簡介——蒙泰爾,
概念
茹利亞方向(Julia direction)是指函式值分布的奇異方向。對於超越整函式(或超越亞純函式),茹利亞方向是複平面C內由原點出發的具有下述性質的半射線J={z|arg z=θ0}:在以J為平分角線的任意小開度的角域內,若是整函式情形,函式取每一有窮值無窮多次,至多除去一個例外;若是亞純函式情形,函式取每一值無窮多次,至多除去兩個例外。茹利亞(Julia,G.M.)於1919—1921年套用蒙泰爾(Montel,P.A.)創立的正規族理論證明,任一超越整函式至少存在一條茹利亞方向。對於亞純函式的情形需要對函式f(z)的增長性加上某些條件,例如滿足:
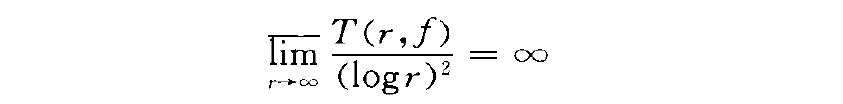
的亞純函式存在一條茹利亞方向,其中T(r,f)是f(z)的奈望林納特徵函式。例如正負實軸是sin z的茹利亞方向。
整函式
整個複平面C內的全純函式.多項式是整函式的特殊情形.不是多項式的整函式稱為超越整函式,例如:
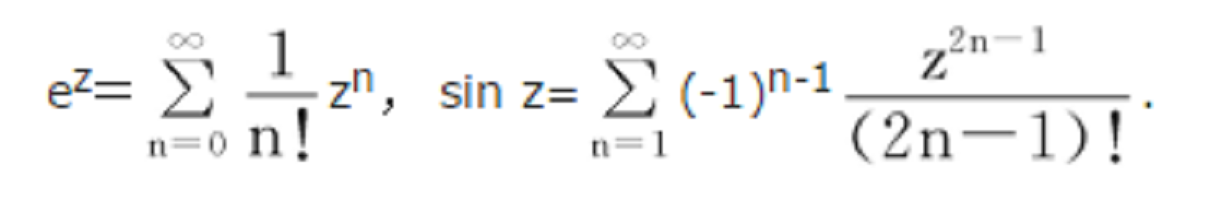
此外,兩個整函式的和、差、積是整函式,又若分母恆不為零時,兩個整函式的商仍為整函式。整函式可看成多項式的自然推廣。代數基本定理指出,p次多項式在複平面內恰有p個根(按重數計算).據此,每一多項式有惟一的乘積表示,即:
f(z)=a(z-z1)…(z-zp),
其中a為非零常數,z1,z2,…,zp是f(z)的零點.反之,總能構造一多項式使得它恰有事先給定的零點和相應的重級,它能表示為乘積的形式,且除去一常數因子之外是惟一確定的.此外,多項式的次數p還能給出|f(z)|增長速度的度量,即當|z|→∞時,有:
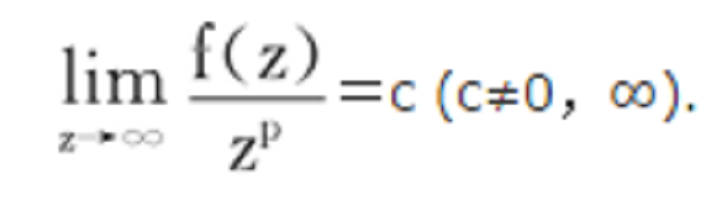
在整函式的研究中,常以多項式為模型提出並討論相應的問題,而獲得類似的結果。
整函式的一般理論源於1876年外爾斯特拉斯(Weierstrass,K.(T.W.))的工作,他的兩個基本定理成為這一理論的出發點.他的第一個定理是關於整函式的因子分解的(參見“魏爾斯特拉斯第一定理”).1882-1884年,拉蓋爾(Laguerre,M.)引入整函式的格這一新的概念,以此來區分整函式的類,整函式的格在某種意義下類似於多項式的次數.1883年,龐加萊(Poincaré,(J.-)H.)建立了整函式的最大模:
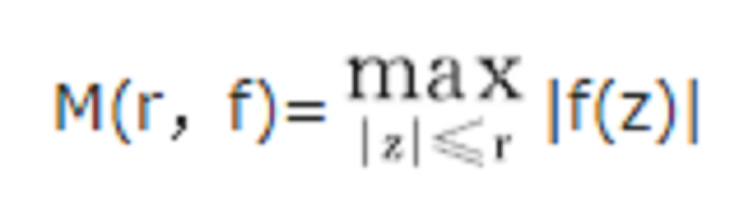
與格的一個關係,即格為k的整函式滿足:
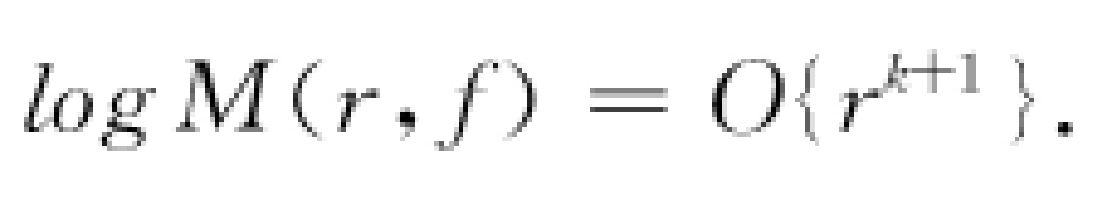
隨後,1893年,阿達馬(Hadamard,J.(-S.))得到一系列結果,它們合起來構成了龐加萊定理的反命題。另一方面,1897年,波萊爾(Borel,(F.-É.-J.-)É.)給出了整函式的級的一個定義。整函式f(z)的級為:
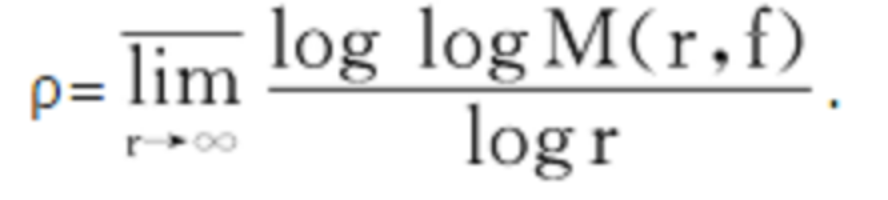
外斯特拉斯的第二個定理是關於值分布的。1879年,皮卡(Picard,(C.-)É.)用橢圓模函式的方法證明了下述重要而深刻的定理:如果一整函式f(z)不取兩個有窮值,則f(z)為一常數。1896年,波萊爾給出了皮卡定理的一個初等證明.他還證明,每一個有窮ρ級的整函式,下式對所有a∈C成立:
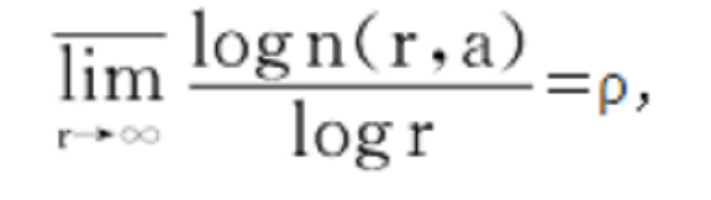
至多除去一個例外的a,其中n(r,a)是圓盤{z||z|≤r}內f(z)的a值點個數,並按重級計算。
20世紀的前20年,波萊爾的結果是整函式理論中最高的成就。它使皮卡定理定量化,而且波萊爾定理中考慮的是函式的a值點數而不是龐加萊定理和阿達馬的結果中所考慮的零點數。這一點還顯示出有窮級整函式值分布的對稱性。在此意義下,它與多項式的結果是相似的。在整函式理論發展過程中,威曼(Wiman,A.)、瓦利隆(Valiron,G.)、林德勒夫(Lindelo¨f,E.L.)等人的工作也很活躍,並做出了許多貢獻。20世紀20年代,奈望林納(Nevanlinna,R.)創立了很廣泛的亞純函式值分布理論,它包括了整函式的經典結果作為其特殊情形,而且形式更為精美。
亞純函式
除極點外為全純的函式為亞純函式,它是複變函數論研究的主要對象之一。
德國數學家外爾斯特拉斯、瑞典數學家米塔-列夫勒、法國數學家柯西等都是亞純函式理論的奠基人。1876年,外爾斯特拉斯證明了一個亞純函式可以表示為兩個整函式的商。第二年,瑞典數學家米塔-列夫勒推廣了外爾斯特拉斯的結果,證明在任意一個區域上的亞純函式皆可表示為兩個函式的商,其中每一個都在該區域內解析。法國數學家柯西也曾給出一種分解方法,對相當廣的一類亞純函式得到簡單的表示式。
近代亞純函式理論是20世紀20年代由芬蘭數學家奈望林納所創立。他在1925年發表了亞純函式的一個一般性理論,這個理論中有兩個基本定理分別被稱為第一基本定理和第二基本定理,從它們可以推出一系列關於亞純函式的值分布的結果,豐富並推進了前人的工作,產生了深遠影響。
亞純函式的術語是由法國數學家布里奧和布凱共同引進的。
人物簡介——蒙泰爾
法國數學家。生於尼斯(Nice)。巴黎大學教授。1937年被選為巴黎科學院院士。主要貢獻在解析函式論和拓撲學方面。在解析函式論中、他引進了“正規函式族”的概念,給出了解析函式族是正規族的條件的“蒙泰爾定理”。主要著作有《正規解析函式族及其套用》(Lecons sur lesfamilles normales de fonctions analytiques et leurs applications,1927)和《單葉和多葉函式》(Lec-ons sur les fonctions univalentesou multivalentes,1933)。線上性拓撲空間中。他建立了所謂蒙特爾空間,簡稱(M)—空間。根據他的貢獻,法國許多大學和其它國家的一些大學都授予他榮譽博士稱號。
