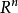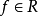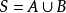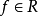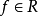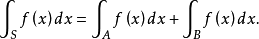若爾當容度

若爾當容度(Jordan content)是長度(或面積、體積)概念的一種推廣。若爾當容度具有非負、單調、有限可加及在正交變換下(可測性及容度)不變等性質。它是由佩亞諾(Peano，G.)於1887年、若爾當(Jordan，M.E.C.)於1892年提出的。若爾當在其1893年出版的《分析教程》中對它作了詳細闡述，提出的目的主要是為了完善黎曼意義下的二重積分理論。黎曼積分只能在若爾當可測集上進行。若爾當容度是與黎曼積分相適應的，它的局限性在於，可測集類不夠廣泛和只有有限可加性(例如有理點集就是不可測的)，這也說明了黎曼積分的局限性。

基本介紹

• 中文名：若爾當容度
• 外文名：Jordan content
• 所屬學科：數學
• 所屬問題：數學分析(積分學)
• 提出者：佩亞諾、若爾當

基本介紹

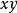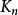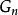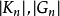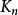若爾當容度是長度(或面積、體積)概念的一種推廣，以平面情形為例，設A為 平面上的有界點集，先用平行於x軸和平行於y軸的直線，將 平面分為邊長為1的閉正方形格線，第二次再將這每個正方形分為四個大小相同的閉正方形，如此下去，用 表示至少含A的一個點的那些第n次所得閉正方形組成之集，用 表示第n次得到的正方形中全部含於A的那些組成之集，並且用 分別表示 和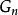 中的閉正方形的面積之和。數 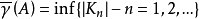和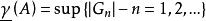 分別稱為A的外容度和內容度。當A的內、外容度相等時，A稱為若爾當可測，這個公共值稱為A的若爾當容度，簡稱容度，記為 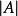。對直線上以及一般 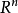中的集合可以類似地定義它的可測性及容度。可以證明，一個集合在若爾當意義下可測與否以及可測時的容度數值，與上述定義中的分法及坐標軸方向無關。

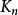
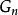
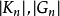
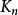
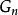
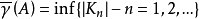
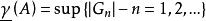
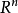
相關性質

定義1設S是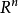的一個緊區間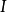的一個子集．對於的每個劃分P定義了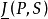是P的只包含S的內點的那些子區間的測度的和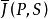，是P的包含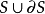的點的那些子區間的測度的和。下面兩個數

分別稱為S的(n維)若爾當內容度和若爾當外容度，集合S稱為是若爾當可測的，如果。在S若爾當可測的情況下， 的這個共同值稱為S的若爾當容度， 用來表示。

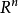
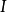
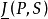
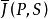
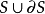
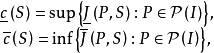
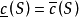
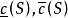
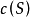
容易驗證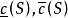僅依賴於S，而不依賴於包含S的區間，而且有。

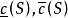
如果S有零容度，則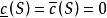。於是，對於每一個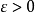，S可以被區間的一個有限族覆蓋，該有限族中各區間測度之和。注意零容度是用有限覆蓋的語言來描述的，而零測度是用可數覆蓋的語言來描述的。任何有零容度的集合也有零測度，但是反過來說則未必成立。

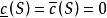
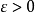
每一個緊區間Q都是若爾當可測的，而且它的容度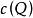等於它的測度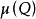。如果k<n，則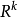內的每一個有界集的n維容度都是零。

內的若爾當可測集S也稱為有面積。在這種情況下，和分別表示從S的“內部”與“外部”對S的面積的逼近，這在圖1中進行了描繪，圖中帶有淺色陰影的矩形算在內，帶有深色陰影的矩形算在了內。對於內的集合，也稱為S的體積。

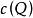
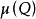
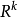
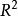
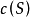
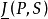
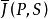
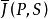
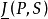
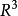
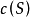
圖1

下面這個定理表明一個有界集有若爾當容度若且唯若它的邊界不是太“厚”。

定理1 設S是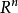內的一個有界集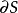，表示它的邊界，則有

於是S是若爾當可測的，若且唯若有零容度。

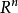
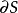
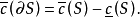
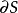
定理2 設S是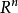內的一個若爾當可測集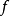，在S上定義且有界，於是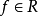於S，若且唯若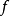在S內的不連續點構成一個零測度集。

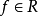
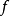
定理3 設S是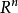內的一個緊的若爾當可測集，於是積分,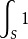存在，而且有

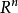
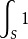
下面這個定理表明黎曼積分關於有若爾當容度的集合是可加的。

定理4 假定在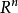內的一個若爾當可測集S上有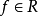，假設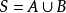，其中A與B都是若爾當可測的，但是它們沒有公共的內點．於是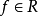於A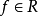，於B，而且有