在現代化的艦船上, 有很多通導設備, 都需要導航數據作為自動控制或測量、顯示用, 這些導航數據( 主要指航向、縱搖、橫搖、航速等) 的準確傳送是上述系統正常工作的基礎, 也是艦船安全航行的保證。
航向數據是重要的導航數據之一, 在大多數情況下它由電羅經提供, 並由航向再傳送裝置輸出。
基本介紹
- 中文名：航向數據
- 外文名：course data
- 數據精度影響：陀螺儀自身漂移誤差、結構形變等
- 地位：重要的導航數據之一
- 輸出：由航向再傳送裝置輸出
- 套用學科：船舶與海洋工程、航空宇航科學
基本介紹,混沌特性,功率譜分析,主分量分析,最大指數,去噪,再傳送裝置,硬體結構,軟體結構,
基本介紹
在現代化的艦船上，有很多通導設備，都需要導航數據作為自動控制或測量、顯示用，這些導航數據(主要指航向、縱搖、橫搖、航速等)的準確傳送是上述系統正常工作的基礎，也是艦船安全航行的保證。
航向數據是重要的導航數據之一，在大多數情況下它由電羅經提供，並由航向再傳送裝置輸出。目前國內船用電羅經航向再傳送裝置主要是由自整角機帶動分羅經來顯示航向，其輸出的航向信號為模擬量，這種形式的航向信號已不能滿足現代化艦船的船用設備對導航數據提出的要求。航向數據的準確性與艦船安全航行息息相關，其數據精度取決於陀螺儀自身的漂移誤差、結構形變以及濕度、溫度等參量，並且與之存在著顯著的非線性關係。
混沌特性
航向數據的準確性與艦船安全航行息息相關，其數據精度取決於陀螺儀自身的漂移誤差、結構形變以及濕度、溫度等參量，並且與之存在著顯著的非線性關係。通過分析數據，判斷系統運動特性，短時預測系統行為，進而為修正系統誤差提供基礎。目前以參數辨識為主的分析方法需要通過理想化部分參量的數值進而簡化原系統建模，顯然降低了模型對原系統的擬合度。混沌特性分析理論為解決這類非線性問題提出了一種新方法。慣導航向輸出數據可以看作是一個多種相關量綜合作用下的非線性混沌時間序列，輸出數據通常會表現出極其複雜而難以長期精確預測的演化特徵，利用混沌理論中的相空間重構方法，可將輸出數據時間序列擴展到高維相空間，體現時間序列信息後再進行短時預測。
由於測量原理及工具的限制，使得時間序列不可避免地帶有噪聲。因此如何將服從一定規律的信號（如混沌信號）與無規律的噪聲相區分是分析時間序列特性的關鍵。分析混沌時間序列的方法主要有主分量分析方法、功率譜分析方法、最大Lyapunov指數法、龐加萊截面法、飽和關聯維數法等，由於這些方法都是從某一方面對序列進行判別，是判斷序列是否混沌的必要條件，因此需要採取多種方法結合的方式，以確保判別的準確性。下面採用功率譜分析方法、主分量分析方法和最大Lyapunov指數方法分別分析航向數據時間序列的特性。
功率譜分析
在一些物理現象中，頻率f與相應的功率E(f)之間具有指數關係，功率譜的冪函式形式表明，雖然頻率f在空間中跨越很寬的尺度，但其結構卻有自相似的特徵，因此，看上去不規則的時間序列圖像，其功率譜卻可能呈現出規則性。一般地，功率譜具有單峰（或多個峰）的譜圖對應於周期序列（或擬周期序列）；無明顯的峰值或峰連成一片，則對應於湍流或混沌序列。所以，可用功率譜分析作為判斷序列混沌的一種方法。
圖是航向數據時間序列功率譜分析圖，從圖中可以看出，航向數據時間序列的功率譜圖無明顯峰值，表明該時間序列具有混沌特性。
航向數據功率譜圖
航向數據功率譜圖主分量分析
主分量分析（PCA分布）方法是近年來提出的一種能有效識別與分析混沌和噪聲的方法，由於混沌信號和噪聲的主分量分布之間存在著顯著差異，混沌信號的主分量譜圖是一條近似直線（或含有類似直線的部分），其斜率為負值且過定點，而噪聲信號的主分量譜圖是一條與x軸接近平行的直線，所以可用於判斷所採集的航向數據時間序列是否為混沌時間序列。
最大指數
以上兩種方法是通過定性分析判斷混沌特性的，而最大Lyapunov指數方法則通過定量分析判斷混沌特性。混沌運動具有初值敏感性的特點，因此即使兩個初值較為靠近，隨著時間的推移，其產生的軌道仍會按指數方式分離，這一現象可採用Lyapunov指數定量描述。若最大Lyapunov小於零，意味著初始相鄰點經疊代後最終要靠攏合併成一點，對應於穩定的不動點或周期運動；若最大Lyapunov大於零，意味著相鄰點最終要分離，對應於軌道的局部不穩定，或在整體穩定因素作用下反覆摺疊形成混沌吸引子。因此，最大Lyapunov指數可作為判斷時間序列混沌特性的一個條件。
去噪
電控羅經是艦船海上航行時的主要航行工具，但是實際套用中由於多種干擾噪聲的存在造成陀螺羅經指向精度不高，如何抑制這些誤差對提高羅經指向精度有著極其重要的意義。建立包括陀螺儀隨機漂移在內的羅經誤差模型，運用Kalman濾波器進行估計，是對各種誤差線上補償的有效途徑。然而經典的Kalman濾波理論是在假設系統動態過程和測量噪聲的先驗統計信息已知的情況下得到的，這使得傳統的Kalman濾波在實際套用中有一定的局限性。
由經典卡爾曼濾波理論可知，經典的卡爾曼濾波是建立在H2估計準則基礎上的，它要求準確的系統模型和確切已知外部干擾信號的統計特性。而在本課題的研究中可知，電控羅經航向數據中存在各種誤差影響，其統計特性是難以確切知道的。
建立的離散狀態空間模型由下列狀態方程和測量方程描述：
式中Xk為k時刻系統狀態;φk+1,k為狀態轉移矩陣;Wk為系統噪聲;Zk為k時刻量測值;Hk為量測矩陣;Vk為量測噪聲在利用經典卡爾曼濾波過程中,由於系統噪聲和量測噪聲是不確切知道的,均假設為白噪聲,設統計特性Q=1,R=1。
將上述算法套用於電控羅經的數據處理中,採集的數據為1000～1200在同一海域所測,海況4級,採樣間隔0.25ms。結果如圖所示。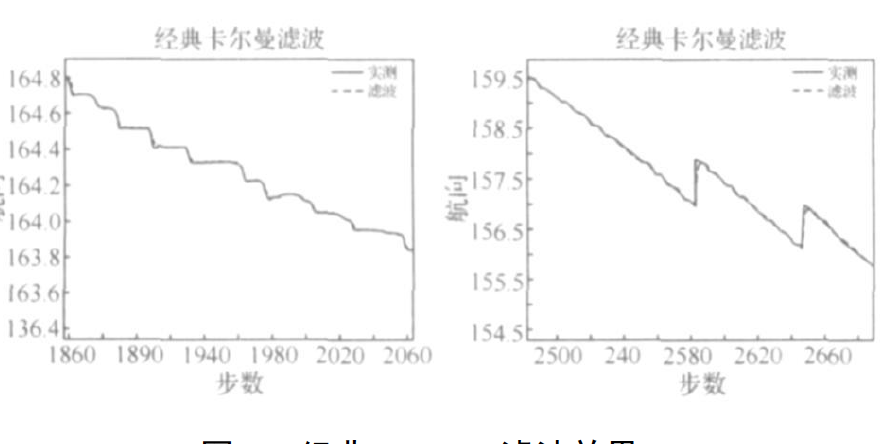
經典Kalman 濾波效果
經典Kalman 濾波效果再傳送裝置
硬體結構
航向數據再傳送裝置硬體電路如圖所示:
航向數據再傳送裝置電路原理DH—3/CLZ—Ⅱ航向數據再傳送裝置電路由兩大部分組成，第一部分是軸角—數字轉換電路，第二部分是航向數字碼讀取、換算與再傳送電路。
1)軸角—數字轉換電路
船舶航行過程中，當航向發生變化時，DH—3型電羅經輸出的航向角經360:1的齒輪組升速，帶動自整角機轉子轉動，輸出航向變化增量。
轉子每轉動一周，對應羅經航向變化1°，其原理如圖所示:
航向輸出原理
航向輸出原理圖中的激磁電壓um，與自整角機交流繞組的三相電壓分別為:
式中:Vm——激磁電壓幅值;
k——自整角機初、次級電壓比;
ω——激磁電壓角頻率;
θ——轉子相對定子空間位置角。
從式中可知，自整角機輸出代表航向變化的三相電壓在時間上都具有sin時的形式，其幅度和相位受轉子角位置θ的調製，即受sinθ、sin(θ+120°)、sin(θ+240°)的調製。
2）航向數字碼讀取、換算與再傳送電路
航向數字碼讀取，換算與再傳送電路是以8031為核心的專用單片機電路。
8031單片機從lP口讀入軸角—數字轉換電路輸出的軸角變化數字編碼，然後根據對照關係，執行專用程式模組將軸角變化換算成航向變化(每一次軸角狀態編碼變化對應航向變化5'，即1/12度)，最後將累積計算後的航向數據以AscⅡ碼形式，通過8031單片機的TxD端和MC1489電平轉換器，按RS—232C標準連續、實時地傳送出去。
軟體結構
航向數據再傳送裝置的軟體由3個程式模組組成:
1)主程式模組;
2)航向數據編碼讀取、換算、診斷累積計算與代碼轉換子程式模組;
3)ASCⅡ碼形式航向數據傳送中斷子程式模組
1、主程式模組
主程式的功能主要是初始化設定，設有兩級中斷，在INTO中斷子程式里主要完成航向數據編碼的讀取、換算診斷、累積計算及代碼轉換，在串列傳送中斷子程式里主要完成ASCI碼形式的航向數據傳送，且設INTO中斷的優先權高於串列傳送中斷。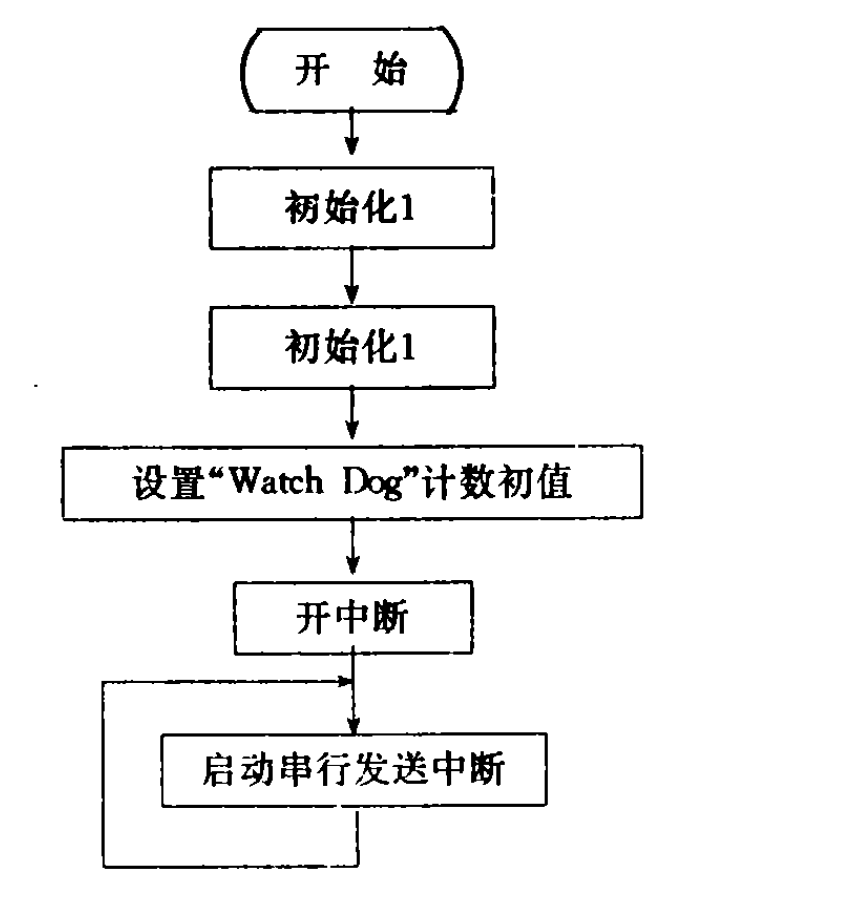
主程式流程圖
主程式流程圖2、航向數據編碼讀取、換算、診斷、累積計算及代碼轉換子程式
該中斷子程式如圖所示。
編碼讀取、換算、診斷、累積計算及代碼轉換程式3、航向數據傳送中斷子程式
進入串列傳送中斷子程式後，首先判斷是否已採集過軸角編碼數據，即判斷第一次NITO標誌是否置位，若設定位，說明自整角機三相電壓沒接入或接入相序有錯，則傳送“告警指示數據塊”，若已置位，說明已採集到軸角編碼數據，則傳送“航向數據塊”。
