棄九法（又稱去九法，舍九法），在中國古代算書中也叫“九減”“九除”“身數除”，在外文文獻中被稱為cast out nines或balances。棄九法是一種檢驗正整數間加減乘除等計算的方法。檢驗時需要分別求得參與運算數字及運算結果的棄九數，用棄九數代替原運算中的數字，檢驗新的計算結果的棄九數是否等於原運算結果的棄九數，兩者不相等說明運算結果一定錯誤，相等說明結果有可能正確。棄九數的本質是一個數字除以九的餘數。棄九法屬於今天初等數論的同餘理論。
基本介紹
- 中文名：棄九法、去九法、舍九法、九減、九除、身數除
- 外文名：cast out nines、balances
- 所屬學科：初等數論
- 理論基礎：同餘理論
操作方法,棄數的求取,檢驗的方法,原理,發展簡史[2],局限性,在現代的意義,數學教育,校驗碼,
操作方法
棄數的求取
棄九數
棄九數的本質是一個數字除以9的餘數，最早烏格里迪西（Abu'l Hasan Ahmad ibn Ibrāhīm Al-Uqlīdisī，約920-約980）給出的求取方法是用需要求棄九數的數字重複多次減去9。烏格里迪西還給出了棄九數的簡單算法，即將一個數字每一位上的數字相加，所得的數字如果超過一位，則繼續將每一位上的數字相加，直到剩下一個一位數為止，這個一位數就是那個數字的棄九數。例如要求取86767的棄九數，就可以計算8+6+7+6+7=34，34是兩位數，因此繼續計算3+4=7，此時7就是86767的棄九數。
棄七數
棄七數的本質是一個數字除以7 的餘數，但具體操作中存在簡便算法，下面以24059為例展示棄七數的簡便求取方法：
先將24059從最高的兩位處斷開，得到24和059，求24除以7的餘數，得到3；將後面數字的最高位也就是0接上去，得到30和59，求30除以7的餘數，餘數是2；將後面數字的最高位也就是5接上，得到25和9，求25除以7的餘數，得到4；把後面的數字也就是9接上得到49，求49除以7的餘數，餘數為0，0即為24059的棄七數。
棄數的選擇與其他可行的棄數
理論上能夠用於檢驗的棄某數可選擇性很大。義大利數學家斐波那契（Fibonacci）所著的《計算之書》（Liber Abaci，1202）中就使用過棄七法、棄九法、棄十一法、棄十三法和棄十七法等多種棄法，但考慮到檢驗效率，目前日常檢驗較為常用的方法仍然是棄九法和棄七法。
檢驗的方法
棄九法可以套用在正整數間加、減、乘、除、開方以及分數乘法的檢驗中，其具體做法如下：
正整數加法
利用棄九法檢驗正整數加法時，需要先求出每個加數的棄九數，再將這些棄九數相加，對得到的數字再求棄九數，將其與原加法的和的棄九數進行對比，兩個數字不同說明計算一定錯誤；兩數相同說明計算有可能正確。
例如要利用棄九法檢驗加法1954+2658=4612，先計算出加數和計算結果的棄九數，分別是1、3和4，將加數的棄九數帶入原先的計算中，得到1+3=4，4與原計算結果的棄九數相等，說明這個加法計算可能是正確的。
正整數減法
利用棄九法檢驗正整數減法時，只需要分別求出被減數、減數、差的棄九數，用被減數的棄九數減去減數的棄九數，對新得到的差再求棄九數，將原差的棄九數與新差的棄九數進行對比，兩個數字不同說明計算一定錯誤；兩數相同說明計算有可能正確。
檢驗減法86767-7485=79282時，需要分別求出被減數、減數和差的棄九數，得到7、6和1，將被減數與減數的數棄九數帶入減法計算中有7-6=1，原減法計算差的棄九數也是1，說明計算有可能是正確的。
正整數乘法
利用棄九法檢驗正整數乘法時，只需要分別求出乘數和乘積的棄九數，將乘數所有的棄九數相乘，對新得到的乘積再求棄九數，將原乘積的棄九數與新乘積的棄九數進行對比，兩個數字不同說明計算一定錯誤；兩數相同說明計算有可能正確。
以乘法9876×5432=53646432為例，乘數的棄九數分別是3和5，乘積的棄九數是6；將兩個乘數的棄九數帶入乘法中，有3×5=15，1+5=6，這與原乘積的棄九數相等，因此計算有可能是正確的。
正整數除法
由於除法存在除不盡的可能性，利用棄九法檢驗正整數乘法時需要考慮餘數的情況。餘數為零時，先求出被除數、除數、商的棄九數，再將除數和商的棄九數相乘，對乘積求棄九數，將乘積的棄九數與被除數的棄九數對比，兩個數字不同說明計算一定錯誤；兩數相同說明計算有可能正確。
例如，249508÷931=268，被除數、除數和商的棄九數分別是1、4和7，將除數與商的棄九數相乘，有4×7=28，其乘積的棄九數是1，這與被除數的棄九數相同，因此計算有可能是正確的。
餘數不為零時，則需要分別求出被除數、除數、商的棄九數，將除數和商的棄九數相乘，對乘積求棄九數，再將求得的棄九數與餘數相加，對相加的和再求棄九數，將最後求得的棄九數與被除數的棄九數對比，兩個數字不同說明計算一定錯誤；兩數相同說明計算有可能正確。
例如，264857除以475，商是557，餘數282。被除數的棄九數是5，除數的棄九數是7，商的棄九數是8；7乘以8得到56，56的棄九數是2；給2加上餘數282得到284，求得其棄九數是5，這和被除數的棄九數一致，因此計算有可能正確。
正整數開方
對於完全平方數，要檢驗其開方結果的正確性，只需要求出被開方數字的棄九數和所開出的正整數根的棄九數，對所開出根的棄九數求平方，再對這個平方求棄九數，將新得到的棄九數與原先被開方的數字的棄九數對比，兩個數字不同說明計算一定錯誤；兩數相同說明計算有可能正確。
例如對116281開方得到正整數根341，檢驗時分別求出被開方數和正整數根的棄九數，即1和8，計算正整數根的棄九數的平方，得到8=64，其棄九數是1，這與被開方數的棄九數相等，因此開方計算有可能是正確的。
對於非完全平方數，開方之後會有餘數產生，利用棄九法檢驗這類開方計算時，需要求出被開方數的正整數根的棄九數，對所開出根的棄九數求平方，求出這個平方的棄九數，再給這個棄九數加上開方時得到的餘數，對兩者的和求棄九數，最後對比這個棄九數和被開方數字的棄九數是否一致，不一致說明計算一定錯誤；一致說明計算有可能正確。
例如，要對67548開平方，得到的正整數根是259，餘數是467。先求出67548的棄九數是3，259的棄九數是7；7=49，49的棄九數是4；我們給4加上餘數467，兩者和的棄九數是3，這和被開平方的數字的棄九數是一樣的，因此這個開方計算有可能正確。
帶分數乘法
利用棄九法檢驗帶分數乘法計算時，先將帶分數進行通分，只考慮分子部分，分別求出兩乘數分子部分的棄九數，將兩者相乘，對乘積再求棄九數，記為A；求出乘積分子部分的棄九數，記為B；將A與B比較，兩個數字不同說明計算一定錯誤；兩數相同說明計算有可能正確。
以
為例，要利用棄九法檢驗這個計算，先將乘法轉化為
，分別求出兩乘數分子部分的棄九數即2和2，將兩者相乘得到4，記為A；對乘積4225求棄九數得到4，記為B，對比發現A、B一致，因此計算可能正確。
原理
棄九法主要是套用了同餘原理，現以正整數乘法
為例對棄九法的原理進行證明：
對於正整數乘法，令
那么上面所求得的乘積是錯誤的。
發展簡史[2]
棄九法最早出現在10世紀阿拉伯數學家烏格里迪西的《印度算術書》（the Kitāb al-fusūl fī al-hisāb al-Hindī, 952/3）中，烏格里迪西介紹自己是首先使用這種檢驗方法的人，目前的史料也支持這一觀點。《印度算術書》將這一檢驗方法套用在對正整數、四則運算、開方、分數計算和一些印度、阿拉伯特殊算法的檢驗中。作者給出了棄九數求取的一般方法和簡便方法，同時也指出了棄九法檢驗存在的缺陷，並列舉了其失效的情況。
此後，棄九法在阿拉伯世界得到了廣泛傳播與套用。15世紀初阿拉伯世界最優秀的數學家之一阿爾·卡西（Ghiyāth al-Dīn Jamshīd Mas'ūd al-Kāshī，約1380-1429）從適合十進制的棄九法中發展出了適合六十進制的棄五十九法，他將這一方法套用在求取圓周率的運算中，這體現出卡西對棄數驗法有效性和實用性的認可。
13世紀初，義大利數學家斐波那契所著的《計算之書》將阿拉伯算術知識介紹到了歐洲，棄九法也隨之傳入了歐洲。除了棄九法外，《計算之書》中還介紹了棄七法、棄十一法、棄十三法以及棄十七法等多檢驗方法。斐波那契使用的求取棄七數的方法也來自阿拉伯。
《計算之書》中的數學內容在歐洲產生了深遠的影響，此後的許多數學作品中都會使用棄數法進行檢驗，但這些著作都不再追求棄數的多樣性，一般只介紹棄九法和棄七法。法國數學家許凱（Nicolas Chuquet，約1455 -1488）的《算術三編》（Triparty en la Sciences des Nombres，1484）、義大利數學家帕喬利(Luca Pacioli，1445-1517)的《算術、幾何、比和比例概要》（Summa de arithmetica, geometria, proportioni et proportionalita，1494，又簡稱《數學大全》）等歐洲數學著作都會在計算時附上利用棄九法、棄七法。
16世紀中期，為了應對宗教改革帶來的衝擊，教皇保羅三世（Pope Paul III，1534-1549在位）批准成立了耶穌會（Society of Jesus）。1582年耶穌會派遣義大利傳教士利瑪竇（MatteoRicci，1552年-1610年）前往中國傳教，在華期間利瑪竇將大量歐洲數學、天文作品翻譯成中文，其中便包括德國數學家克拉維烏斯（Christoph Clavius，1537-1612）的《實用算術概要》（Epitome Arithmeticae Practicae，1583）。《實用算術概要中》中演示了棄九法、棄七法的使用方法，作者使用字母X符號來輔助整理棄九數、棄七數，以這部作品為底本編譯而來的《同文算指》(1613)中完整地保留了這些內容，棄九法從而進入了中國。在《同文算指》中棄九法被稱為“九減”“九除”，棄七法則被稱為“七減”“七除”。在明末清初的《太西算要》（1625）、《歐羅巴西鏡錄》等介紹歐洲數學的作品中也都有棄九法和棄七法內容，但對這一檢驗方法的稱呼在不同作品中略有不同。
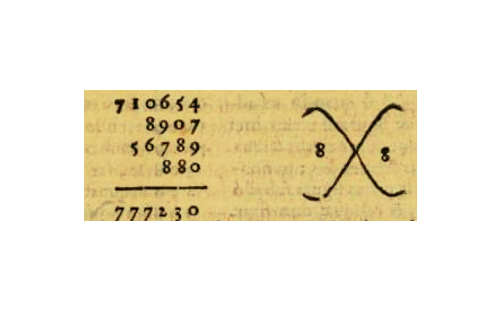
《實用算術概要》中利用棄九法檢驗加法示意圖
《同文算指》中利用棄九法檢驗加法示意圖
清初著名數學家梅文鼎（1633-1721）在《歷算全書之筆算》（1693）中利用棄九法檢驗加減運算時，只採用短豎線整理等式兩端的棄九數，使得這一檢驗方法的書寫更為簡便、直觀。
《歷算全書之筆算》中利用棄九法檢驗加法示意圖
局限性
使用棄九法檢驗計算時，如果最終的棄九數不相等，則此計算一定錯誤；但如果兩次計算的棄九數相等，也不能保證計算一定正確。以乘法574×386=211142為例，兩個乘數的棄九數分別是7和8，乘積的棄九數是2，7×8=56，56的棄九數也是2，這是符合棄九法檢驗的，但是如果將574×386乘積位置的數字換成211412或211232等數字，計算一定發生了錯誤，但由於乘積位置上數字的棄九數仍然是2，棄九法就無法檢驗出這些錯誤。烏格利迪西早在提出棄九法時就注意到了這一問題。
然而，只要按照加、減、乘、除的四則運算法則進行運算，錯誤往往發生在進位、借位、錯位時，這些錯誤比較容易通過棄九法檢驗出來。如果不是刻意去湊數，把的乘積寫成211412或211232等數字的可能性非常小。自棄九法產生以來，這一方法在一千餘年中被多個文明接受並廣泛使用，反覆出現於多部重要的數學著作中，這些數學實踐已經證明棄九法是一種操作簡便且行之有效的檢驗方法。
在現代的意義
數學教育
作為一種簡單有效的檢驗方法，棄九法在中國晚清時期的《直方大齋數學》（1903-1907）、《算術駕說》（1907）等初等數學教科書都有介紹。中國教育部在1952年頒布的《中學數學教學大綱（草案）》中也指出應當讓學生使用棄九法來檢驗演算的結果。近些年，棄九法再次出現在我國高中數學教材選修內容中。
校驗碼
棄九法的發明是為了避免計算中出現的錯誤，但隨著計算器等工具的發展，計算出錯的可能性不斷降低，但輸入數字時仍然存在出錯的可能性，因此編碼學上引入了校驗碼以檢驗輸入數字的正確性。校驗碼被廣泛套用在身份證號碼、全國組織機構代碼、銀行卡號、鈔票號碼、圖書ISBN編號、商品條形碼中，而這些校驗碼的計算大多也會涉及餘數求取。例如，目前我國第二代居民身份證一共18位，將前17位數字與其對應的加權因子相乘，計算其總和，再求出數字總和除以11的餘數，也就是求出它的棄十一數，對這個數進行查表就能得到身份證的第18位數字，這個數字就是身份證號碼的校驗碼。上述校驗碼檢驗與棄九法檢驗思想一致。
