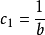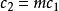自由體積理論

自由體積理論是把液態和固態物質的體積區分為占有體積和自由體積兩部分來解釋液體的粘度與溫度的關係，推導WLF方程和解釋玻璃化轉變機理及其影響因素的一種理論。

在一定的溫度下，液態物質內部處於高彈態的高聚物內的自由體積分數、構成自由體積的孔穴在尺寸和位置上的分布狀態也是一定的。隨著溫度的升降，不但占有體積要熱脹冷縮，而且自由體積也要熱脹冷縮，孔穴的大小及其分布也要進 行調整，以適應所處的溫度。但是當物質處於玻璃態時，只有占有體積能熱脹冷縮，而自由體積則因分子運動和鏈段運動的凍結而被凍結。這一理論把玻璃態視為等自由體積狀態。

基本介紹

• 中文名：自由體積理論
• 外文名：free volume theory
• 提出者：Vrentas和Duda
• 作用：WLF方程和解釋玻璃化轉變機理
• 表征：粘度和溫度之間關係
• 學科：物理學

基本概述

如果使一種可結晶的液體增塑劑冷卻，則它的體積便隨溫度的下降而逐漸減小，直至固化點(結晶點)為止。而在固化點溫度下，增塑劑由液體變為固體時，它的體積會驟然減小，這種現象可用自由體積理論來解釋。冷卻與結晶會使自由體積減小，加熱和熔融則會使體積增加。

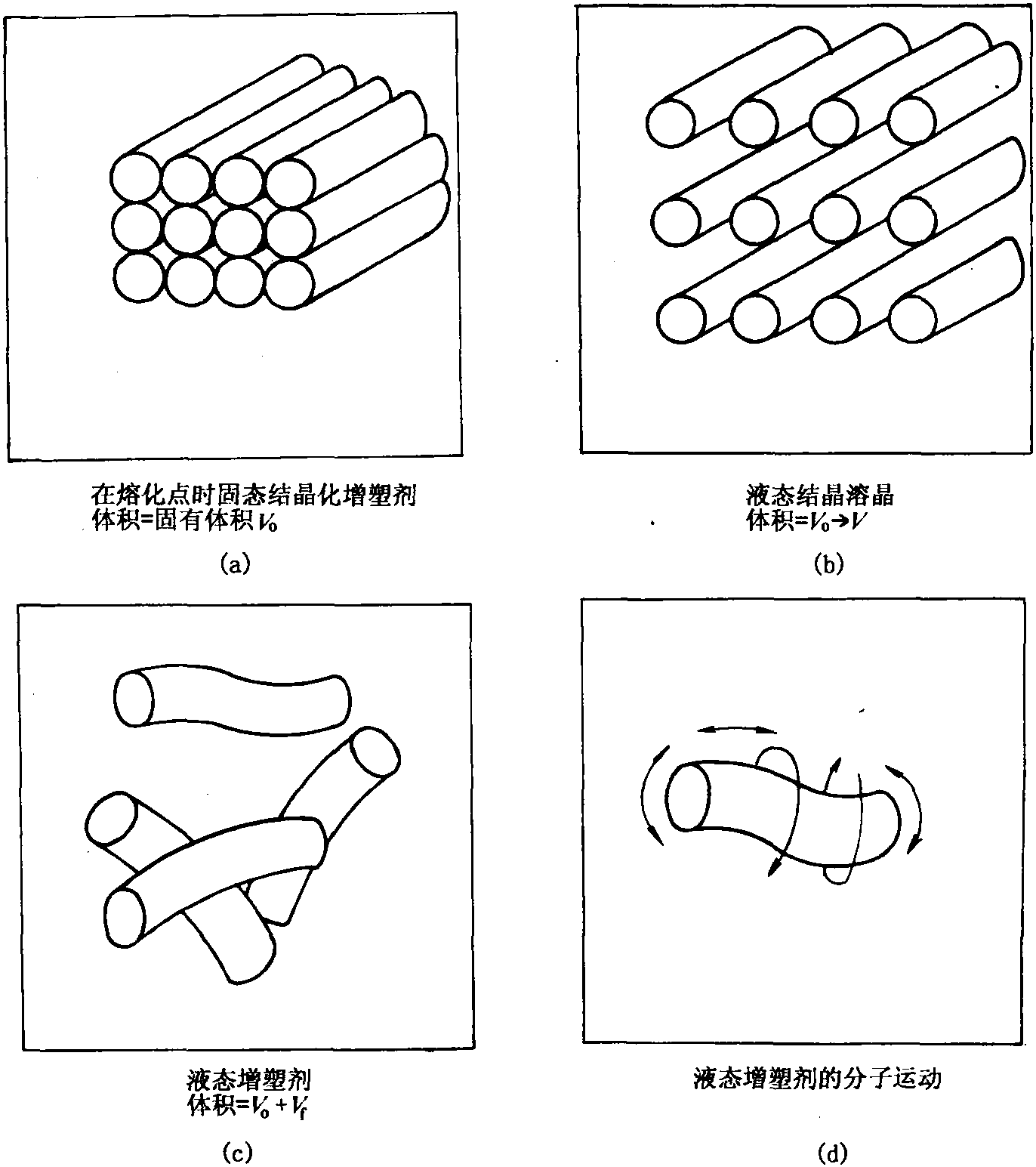
增塑劑由結晶狀態變為液態時，其體積的變化情況如圖1所示。圖中(a)是結晶狀態， 內部分子呈規整而緊密的排列；圖中(b)表示液晶狀態，由於溫度逐漸升高晶體開始分離， 內部分子呈規整而較為鬆散的排列；圖中(c)是增塑劑結晶態在排斥力和熱運動的影響下最 終發生破壞而變為液態的情況，其內部分子呈無規則熱運動，此時體積大大增加，所增加的 體積便是自由體積，它隨溫度的升高而逐漸增大。圖中(d)顯示了液態時分子的各種無規則 運動狀態。圖中V是總體積，V₀為分子規整而緊密時的占有體積，V_f為自由體積。

Ferry運用自由體積這一概念對增塑機理和增塑劑的使用作了說明。他認為在任何溫 度下聚合的流動性主要取決於剩餘自由體積的空間大小。Dootlitle則建立了粘度與自由體積的關係式：

lnn₀=lnA+B(V-V_f)/V_f

式中 n₀——粘度；

A、B——經驗常數，B約等於1；

V——總體積；

V_f——自由體積。

由上式可知，若增大自由體積，則粘度減小，從而流動性增大，這意味著對形變的敏感性增大，這樣便增加了高分子材料的塑性。前面曾經提過，加熱有增塑作用，這是因為溫度提高后，高分子聚合物的自由體積增大的結果。增塑的另一個方法是添加一有較大自由體積的物 質，即增塑劑。小分子比大分子有更多潛在的自由體積，這是因為它們有更多的機會進行活 動，它們的端基有更多的振盪和移動，並且能夠旋轉、扭曲、甚至翻轉，並且通過自己的功能 與其它分子相碰撞。

圖1 增塑劑自由體積示意圖

按照自由體積理論，聚合物與增塑劑均占有自由體積或有產生自由體積的能力，但由於高分子聚合物體積大，且分子運動的運動的空間阻礙也大，熱運動又受到一定的限制，所以這種自由體積是必不可少的，否則聚合物分子便會失去流動性，變得僵硬而難於成形。增塑劑有較大的自由體積，聚合物的分子鏈段可以滲入其內，又由於增塑劑的粘度較低，這樣聚合物與鏈段的流動性就增加，聚合物及其鏈段還可以自由地運動，因為它們比其它聚合物更 容易排開低粘度的增塑劑分子。由此可見，增塑劑的作用是使聚合物鏈有更多餘地進行自由運動。

WLF方程

對瀝青之類能形成玻璃態的物質，其黏度與溫度關係的一種定量表達方法。普通瀝青在低於玻璃態轉變溫度(T_g)之下，呈硬脆的非晶態(玻璃態)。中間相瀝青，如中間相含量達到或近於100%，不是由同向性和異向性兩相組成而是呈單一相態的均一物態，在低於T_g下也呈玻璃態。均一瀝青的黏度溫度關係，原則上可用WLF方程來描述。1955年這一方程首先由威廉士(M.L.Williams)、蘭德爾(R.F.Landel)和費雷(J.D.Ferry)在研究高聚物的黏彈性時提出，所以以三位作者姓氏的第一個字母連綴在一起作為這一方程的名稱。20餘年之後，在對瀝青類物質的有關論述中逐漸套用這一表達式。

在溫度T時的黏度記為η(T)在T_g下的黏度記為η(T_g)，WLF方程取如下形式：

lgη(T)=lgη(T_g)-[c₁(T-T_g)]/{c₂+(T-T_g)} （1）

這一半經驗方程含有兩個由實驗數據確定的參數c₁、c₂。這兩個參數的大小隨瀝青而異，並非常數。瀝青的η(T_g)在10 Pa·s左右，一般常取η(Tg)為1012 Pa·s。對A240瀝青，c1=16.385，c2=35.358，由此可算出175℃、200℃時黏度分別為1.102、0.214Pa·s，進一步計算可得到圖2中A240的黏度一溫度曲線。A240及由A240熱加工得到的QI<1%，不含中間相的同向性瀝青(AC瀝青)，其性能及WLF方程參數，列於表1。

表1 阿士蘭系石油瀝青

性 能	瀝 青
	A240	AC-60	AC-65	AC-70	AC-75	AC-85
TI/%; Tg/℃; 軟化點/℃; WLF參數：c1; WLF參數：c2	6; 79.6; 119; 16.385; 35.358	9; 120.6; 151; 15.387; 25.217	11; 148.8; 177; 16.017; 34.847	25; 170.9; 208; 15.698; 37.865	26; 195.0; 234; 16.586; 46.593	41; 224.4; 266; 16.385; 35.358

由此得到的阿士蘭系瀝青的黏度—溫度關係繪於圖2。

圖2 阿士蘭系瀝青黏度—溫度關係

1—A240；2—AC-60；3—AC-65；4—AC70；5—AC75；6—AC-85

WLF方程中參數的確定方法 方程(1)可改寫為如下形式：

1/{lgη(T_g)- lgη(T)}=(c₂/c₁)(1/T-T_g)+1/c₁ (2)

將在不同溫度下實測瀝青黏度值，以1/[lgη(Tg)-lgη(T)]對1/(T-Tg)作圖，如果瀝青的黏度—溫度關係符合WLF方程，應得到一直線。用最小二乘法對數據進行處理，可得到與實測數據符合得最好的直線斜率m與截距b。由(2)式可知：

， （3）