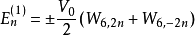概念
自由電子模型將
電子看成
勢場運動,因而可用於模擬能量狀態,用於計算
超晶格中層間交換禍合隨鐵磁層和非
磁層厚度的關係。在相同的參數下,
振盪周期與鐵磁-非磁層的對數有關。而層間藕合隨鐵磁層厚度的變化曲線中存在兩個振盪周期,因而出現
拍頻現象。
分子軌道對稱守恆原理的自由電子模型
分子軌道對稱守恆原理在化學上的套用日益廣泛。 國際上關於這方面的理論主要有: 能量相關理論、前線
分子軌道理論以及
芳香過渡態理論。 它們討論的是
協同反應的選律,結論基本一致。我國科學家唐敖慶對這三個理論有明確的評價,並在理論上有新的發展。
研究的目的在於利用數學上比較簡單、易於理解的“自由電子分子軌道理論”,嘗試用統一的相關圖來表述該原理(並在此基礎上對三個理論的聯繫及存在的某些問題作一些初步的探討),以利於對該理論的理解、普及以及進行教學。
線性共軛分子中的FEMO
共軛分子的主要特徵在於
π電子運動的公有化,而FEMO理論正是簡單、形象地反映了這一特點,抓住了問題的主要矛盾,因而在一定程度上它能簡明地闡述共軛體系的若干性質。而協同反應一般均牽涉到π電子的遷移或共軛體系的變化,從而用FEMO理論來表述分子軌道對稱守恆原理是比較方便的。由於FEMO理論可以統一得到鏈狀共軛體系中各分子軌道能級的相對順序及各軌道的對稱性,這就有可能用它來構成統一相關圖。
 圖 1 FEMO ( 左 ) 與 LCAOMO(右)
圖 1 FEMO ( 左 ) 與 LCAOMO(右)圖1描述了各個分子軌道的能級高低及
波函式的圖形。由於共軛π鍵是由共面原子的
p軌道平行交迭而成的,考慮各軌道的對稱性時必須注意它實際上有上下兩葉。將ф(x)結合p軌道考慮,這與由LCAOMO理論得出的結論基本是一致的,一下討論將按此方式進行。
在波函式表示圖中,分子平面上部Z方向的曲線所代表的ф值為正,下部為負。為方便,把ф(x)畫在能級線En上。
能量相關理論
根據Woodward和Hoffman提出的分子軌道對稱守恆原理中的能量相關理論,可按其相似的方法,用FEMO作出電環化反應的相關圖。首先研究一下FEMO的對稱性質(圖2)。量子數為奇的狀態,對c
2(即二次旋轉軸)的旋轉來說是反對稱的,對m(即鏡面)的反映來說是對稱的。量子數為偶的狀態則反之。
 圖 2 FEMO的對稱性
圖 2 FEMO的對稱性在電環化過程中,體系兩端的兩個p軌道生成一個
鍵,它對於c
2及m而言,始終是對稱的(
反鍵在此可認為是
鍵的激發態,在核間有一節面),原來的共軛體系少了兩個p軌道,共軛鍵長度由l縮短到l’,軌道能量增高。由相關圖,當將體系的電子按照排布規則填充到各軌道後,立即得到電環化反應的選律:(1)(4n+2)電子體系:對旋時反應物與生成物基態間關聯,因而加熱允許。順旋時基態與激發態間關聯,反應需較高活化能,加熱禁阻。(2)4n電子體系:同理可見,對旋加熱
禁阻,光照允許,順旋加熱允許。
二維自由電子模型
根據
共軛體系中
p軌道的共面性質,更宜於用二維模型描述。考慮到共軛體系中通過原子的平面為一節面,由於E
y遠遠大於E
x(因為b遠遠小於l),且當共軛體系長度變化時可認為不引起b的變化可簡化地視為n
y=1,E
y為常量,故只需考慮E
x的改變即可,由此便可直接畫出各分子軌道的圖形。當然用這套圖形來構成相關圖以及用其前線軌道討論問題就比較更直觀,和LCAOMO圖形更接近(圖3)。
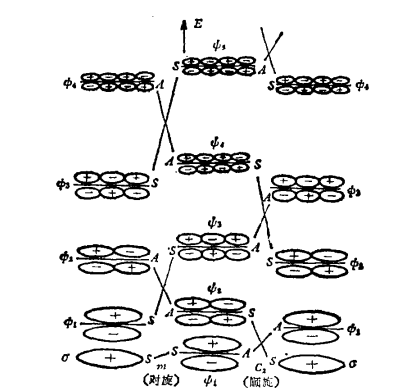 圖3 電環化反應能級相關圖
圖3 電環化反應能級相關圖苯的自由電子模型能級修正的討論
苯的自由電子模型把
電子看成在一個環形勢場中運動,並受到C
6具有
對稱性的微擾作用。研究探討苯的能量至二級修正,得出只在某些特定能級上發生
分裂,簡併完全解除。
確定微擾形式
在苯的自由電子模型中,將
苯粗略地當作有
碳原子組成的一個圓,而電子就在此圓周上運動,當電子在半徑為 R的圓周上運動時,只有一個變數,即角度h,但由於實際上苯的 6個碳原子成一個平面六角形的排列,苯有一個六重軸,苯的對稱性可用 C6 群表示,故電子還應受到 C
6 對稱性的微擾勢作用。
激發態能量的一級修正
不計微擾時,
本徵態(
基態除外)是二重簡併的,即J
(0)n(h)與 J
(0)-n (h )對應同一能量值。考慮微擾作用,求激發態能量的一級修正,先尋求微擾矩陣元,解之得:
即只有當n= ± 3時,能級才完全分裂,n≠± 3時能級一級修正為 0。即在一級修正下,n ≠± 3的能級不分裂。
研究結論
苯的自由電子模型中,對稱性微擾勢使電子能級發生十分有趣的分裂現象:能級修正至一級近似時,n= ± 3能級簡併被解除,n≠± 3時無影響;修正至二級近似時,n= ± 6能級簡併被解除,n≠± 6能級只發生偏移。至此,我們得出結論:在能量修正至二級近似下,微擾只能使 n= 3k (k= ± 1,± 2)的能級發生分裂,簡併解除。並構想如下:在更高級近似下,微擾也只能使 n= 3k(k= ± 1,± 2,Λ)的能級發生分裂,簡併解除。此構想是否正確,尚須予以嚴格證明。另外,在
量子化學中,苯的自由電子模型對處理苯問題也是較為成功的。
 圖 1 FEMO ( 左 ) 與 LCAOMO(右)
圖 1 FEMO ( 左 ) 與 LCAOMO(右) 圖 2 FEMO的對稱性
圖 2 FEMO的對稱性
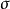
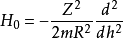
 圖3 電環化反應能級相關圖
圖3 電環化反應能級相關圖