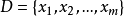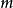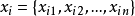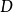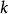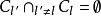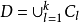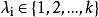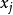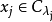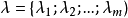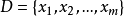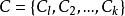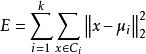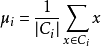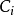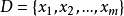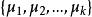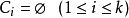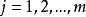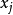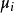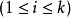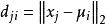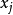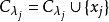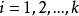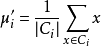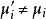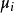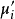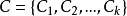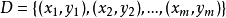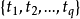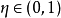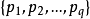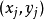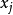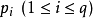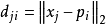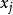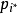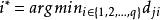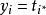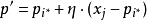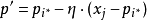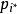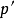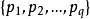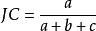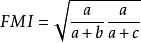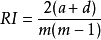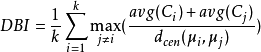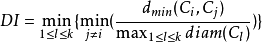自動聚類是一種典型的無監督機器學習（無監督學習）方法。聚類試圖將數據集中的樣本劃分為若干個通常不相交的子集，每個子集稱為一個簇，通過這樣的劃分，每一個簇可能對應一些潛在的概念（類別）。
需說明的是，概念對於聚類算法而言事先是未知的，聚類過程僅能自動形成簇結構，簇所對應的概念語義需由使用者來把握和命名。
基本介紹
- 中文名：自動聚類
- 外文名：Automatic Clustering
- 學科：機器學習
- 基本釋義：將數據集劃分為若干個不相交子集
- 分為：原型聚類;密度聚類;層次聚類
- 套用：人工智慧
基本概念,數學模型,原型聚類,K均值算法,學習向量化,高斯混合聚類,密度聚類,層次聚類,性能度量,外部指標,內部指標,
基本概念
聚類試圖將數據集中的樣本劃分為若干個通常不相交的子集，每個子集稱為一個簇，通過這樣的劃分，每一個簇可能對應一些潛在的概念（類別），如“淺色瓜”、“深色瓜”，有籽瓜“、”無籽瓜“，甚至”本地瓜“、“外地瓜”。
需說明的是，概念對於聚類算法而言事先是未知的，聚類過程僅能自動形成簇結構，簇所對應的概念語義需由使用者來把握和命名。
聚類既能作為一個單獨的過程，用於尋找數據內在的分布結構，也可作為分類等其他學習任務的前驅過程。例如，在一些商業套用中需對新用戶的類型進行判別，但定義“用戶類型”對商家來說可能不太容易，此時往往可先對用戶數據進行聚類，根據聚類結果將每個簇定義為一個類，然後基於這些類訓練分類模型，用於判別新用戶的類型。
基於不同的學習策略，人們設計出多種類型的算法。
數學模型
假定樣本集
包含
個無標記樣本，每個樣本
是一個
維特徵向量，則聚類算法將樣本集
劃分為
個不相交的簇
，其中，
，且
。相應地，我們用
表示樣本
的“簇標記”，即
。於是，聚類的結果可用包含 m 個元素的簇標記向量
表示。
原型聚類
原型聚類亦稱為“基於原型的聚類”，此類算法假設聚類結構能夠通過一組原型刻畫，在現實聚類任務中極為常用。通常情形下，算法先對原型進行初始化，然後對原型進行疊代更新求解。採用不同的原型表示、不同的求解方式，將產生不同的算法。
K均值算法
給定樣本集 ，‘k-均值’ （k-means）算法針對聚類所得簇劃分
最小化平方誤差
最小化平方誤差（上式）並不容易，找到它的最優解需考察樣本集D所有可能的簇劃分，這是一個NP難問題。因此，k 均值算法採用了貪心策略，通過疊代最佳化來近似求解，算法流程如下：
輸入：樣本集
；聚類簇數 k
過程：
1）從 D 中隨機選擇 k 個樣本作為初始均值向量
2）repeat
3) 令
4） for
do
5)計算樣本
與各均值向量
的距離：
6) 根據距離最近的均值向量確定的簇標記：
7） end for
8) for
do
9)計算新均值向量：
10) if
then
11）將當前均值向量更新為
12） else
13) 保持當前均值向量不變
14） end if
15) end for
16) until 當前均值向量均未更新
輸出：簇劃分
學習向量化
與 k 均值類似，“學習向量量化”（Learning Vector Quantization，簡稱LVQ） 也是試圖找到一組原型向量來刻畫聚類結構，但與一般聚類算法不同的是，LVQ假設數據樣本帶有類別標記，學習過程利用樣本的這些監督信息來輔助聚類。
算法流程如下：
輸入：樣本集
；
原型向量個數 q ，各原型向量預設的類別標記
；
學習率
過程：
1） 初始一組原型向量
2） repeat
3） 從樣本集合 D 中隨機選取樣本 
4） 計算樣本
與
的距離：
5) 找出與
距離最近的原型向量
，
6) if
then
7) 
8) else
9) 
10) end if
11) 將原型向量
更新為
12）until 滿足停止條件
輸出：原型向量
高斯混合聚類
與k均值、LVQ用原型向量來刻畫聚類結構不同，高斯混合模型採用機率模型來表達聚類原型。
基本思想：假設整個數據集服從高斯混合分布，待聚類的數據點看成是分布的採樣點，通過採樣點利用類似極大似然估計的方法估計高斯分布的參數。求出參數即得出了數據點對分類的隸屬函式。
密度聚類
密度聚類亦稱為“基於密度的聚類”，此類算法假設聚類結構能通過樣本分布的緊密程度確定。通常情形下，密度聚類算法能夠從樣本密度的角度來考察樣本之間的可連線性，並基於可連線性不斷擴展聚類簇以獲得最終的聚類結果。
DBSCAN是一種著名的密度聚類算法，它基於一組“鄰域”參數來刻畫樣本分布的緊密程度。
具體算法描述如下：
輸入: 包含n個對象的資料庫，半徑e，最少數目MinPts;
輸出:所有生成的簇，達到密度要求。
1) Repeat
2) 從資料庫中抽出一個未處理的點；
3) if 抽出的點是核心點 then
找出所有從該點密度可達的對象，形成一個簇；
4) else
5)抽出的點是邊緣點(非核心對象)，跳出本次循環，尋找下一個點；
5) until 所有的點都被處理。
層次聚類
層次聚類試圖在不同層次上對數據集進行劃分，從而形成樹形的聚類結構。數據集的劃分可採用“自底向上”的聚合策略，也可採用“自頂向下”的分拆策略。
AGNES是一種採用自底向上聚合算法。它先將數據集中的每個樣本看作一個初始聚類簇，然後在算法運行的每一步找出距離最近的兩個聚類簇進行合併，該過程不斷重複，直至達到預設的聚類簇個數。
算法描述：
輸入：包含n個對象的資料庫，終止條件簇的數目k
輸出：k個簇
1) 將每個對象當成一個初始簇
2) Repeat
3) 根據兩個簇中最近的數據點找到最近的兩個簇
4) 合併兩個簇，生成新的簇的集合
5) Until達到定義的簇的數目
性能度量
聚類性能度量，亦稱為聚類“有效性”指標，與監督學習中性能度量類似，對聚類結果，我們需要通過某種性能度量來評估其好壞；另一方面，若明確了最終要使用的性能度量，則直接將其作為聚類過程的最佳化目標，從而更好地得到符合要求地聚類結果。
聚類是將樣本集D劃分為若干個不相干地子集，即樣本簇。那么什麼樣地聚類結果比較好呢？直觀上看，我們希望“物以類聚”，即同一簇地樣本儘可能相似，不同樣本地簇儘可能不同。換言之，聚類結果的“簇內相似度高”且“簇間相似度低”。
聚類性能度量有兩類：一類是將聚類結果與某個參考模型進行比較，稱為“外部指標”；另一類是直接考察聚類結果而不利用任何參考模型，稱為“內部指標”。
外部指標
Jaccard係數（Jaccard Coefficient，簡稱 JC）
上述性能度量的結果值均在[0,1]之間，值越大越好。
內部指標
DB指數（Davies-Bouldin Index，簡稱DBI）
DBI值越大越好，而DI相反，越小越好。
