脈衝回響不變法，也稱衝激回響不變法。是一種將模擬濾波器轉化為數字濾波器的基本方法。它利用模擬濾波器理論設計數字濾波器，也就是使數字濾波器能模仿模擬濾波器的特性，這種模仿可從不同的角度出發。脈衝回響不變法是從濾波器的脈衝回響出發，使數字濾波器的單位脈衝回響序列h(n) 模仿模擬濾波器的衝擊回響ha(t), 使h(n)正好等於ha(t)的採樣值，即h(n)=ha(nT)T為採樣周期。
基本介紹
- 中文名：脈衝回響不變法
- 類別：模擬濾波器轉化為數字濾波器
- 利用：模擬濾波器理論設計數字濾波器
- 概念：數字濾波器能模仿模擬濾波器特性
概念詳解,小結,
概念詳解
如以Ha(s)及H（z）分別表示ha(t)的拉氏變換及h(n)的z變換，即
Ha(s)=L[ha(t)]
H(z)=Z[h(n)]
則根據採樣序列z變換與模擬信號拉氏變換的關係，得:
上式表明，採用脈衝回響不變法將模擬濾波器變換為數字濾波器時，它所完成的S平面到Z平面的變換，正是以前討論的拉氏變換到Z變換的標準變換關係，即首先對Ha(s)作周期延拓，然後再經過z=e^sT的映射關係映射到Z平面上。
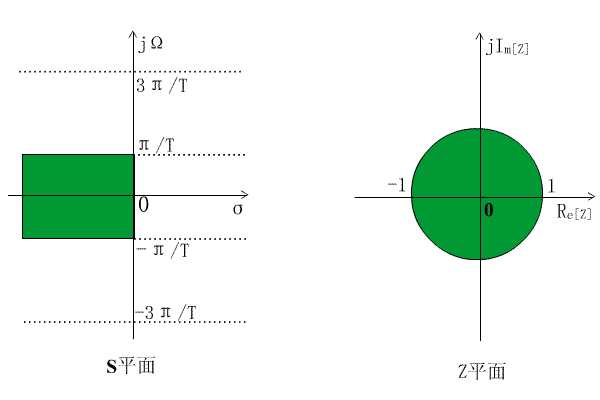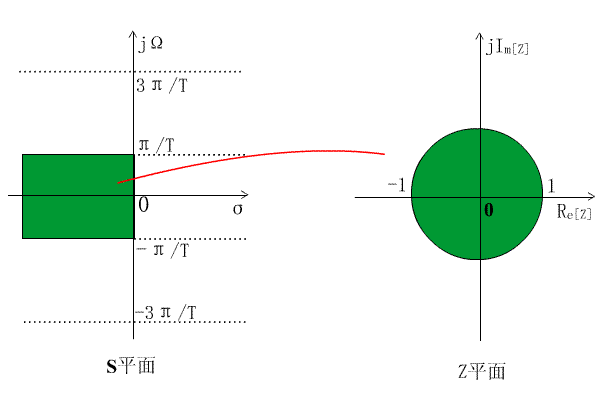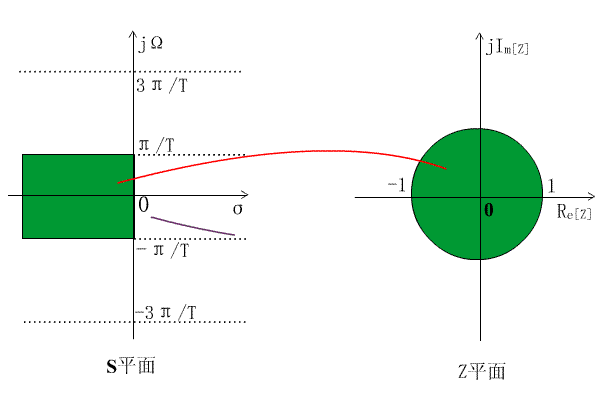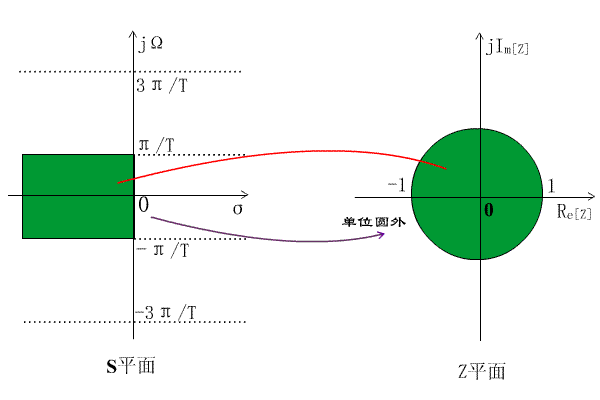
z=e^sT的映射關係表明，S平面上每一條寬為2π/T的橫帶部分，都將重疊地映射到Z平面的整個全部平面上。每一橫帶的左半部分映射到Z平面單位圓以內，每一橫帶的右半部分映射到Z平面單位圓以外，jΩ軸映射在單位圓上，但jΩ軸上的每一段2π/T都對應於繞單位圓一周，如下圖所示：
圖 脈衝回響不變法的映射關係
應當指出，Z=e^sT的映射關係反映的是Ha(s)的周期延拓與H（z）的關係，而不是Ha(s)本身與H（z）的關係，因此，使用脈衝回響不變法時，從Ha(s)到H(z)並沒有一個由S平面到Z平面的簡單代數映射關係，即沒有一個s=f(z)的代數關係式。另外，數字濾波器的頻響也不是簡單的重現模擬濾波器的頻響，而是模擬濾波器頻響的周期延拓，周期為ΩS=2π/T=2πfs，即
正如第一章採樣定理中所討論的，如果模擬濾波器的頻響帶限於摺疊頻率ΩS/2以內，即
Ha(jΩ)=0 |Ω|≥π/T
這時數字濾波器的頻響才能不失真地重現模擬濾波器的頻響（在摺疊頻率以內）
|ω|<π
但任何一個實際的模擬濾波器，其頻響都不可能是真正帶限的，因此不可避免地存在頻譜的交疊，即混淆，這時，數字濾波器的頻響將不同於原模擬濾波器的頻響而帶有一定的失真。模擬濾波器頻響在摺疊頻率以上衰減越大，失真則越小，這時，採用脈衝回響不變法設計的數字濾波器才能得到良好的效果。
脈衝回響不變法特別適用於用部分分式表達的傳遞函式，模擬濾波器的傳遞函式若只有單階極點，且分母的階數高於分子階數N>M，則可表達為部分分式形式：
其拉氏反變換為：
其中u(t)為單位階躍函式。對ha(t)採樣就得到數字濾波器的單位脈衝回響序列
再對h(n)取Z變換，得到數字濾波器的傳遞函式：
第二個求和為等比級數之和， ，要收斂的話，必有 ，所以有
比較部分分式形式的Ha(s)和上式H(z)可以看到，S平面上的極點s=si,變換到Z平面上是極點 ,而Ha(s)與H(z)中部分分式所對應的係數不變。如果模擬濾波器是穩定的，則所有極點si都在S左半平面，即Re[si]<0,那么變換後H(z)的極點 也都在單位圓以內，即| |= <1，因此數字濾波器保持穩定。
值得注意的是，這種Ha(s)到H(z)的對應變換關係，只有將Ha(s)表達為部分分式形式才成立。
雖然脈衝回響不變法能保證S平面與Z平面的極點位置有一一對應的代數關係，但這並不是說整個S平面與Z平面就存在這種一一對應的關係，特別是數字濾波器的零點位置與S平面上的零點就沒有一一對應關係，而是隨著Ha(s)的極點si與係數Ai的不同而不同。
H(e) 是Ha(jΩ)的周期延拓（周期為fs），因Ha(jΩ)並不是帶限，即在超過fs頻率部分並不為0，所以就產生了混迭。當為低通或帶通濾波器時，fs越大，則Ha(jΩ)的下一周期相隔越遠，混迭也就越小。當為帶阻或高通濾波器時，Ha(jΩ)在超過fs/2頻率部分全為通帶，這樣就不滿足抽樣定理，發生了完全的混迭，所以脈衝回響不變法不能設計帶阻或高通濾波器。
小結
- 在要求時域脈衝回響能模仿模擬濾波器的場合，一般使用脈衝回響不變法。
- 脈衝回響不變法的一個重要特點是頻率坐標的變換是線性的，ω=ΩΤ，ω與Ω是線性關係。因此如果模擬濾波的頻響帶限於摺疊頻率以內的話，通過變換後濾波器的頻響可不失真地反映原回響與頻率的關係。
例如線性相位的貝塞爾低通濾波器，通過脈衝回響不變法得到的仍是線性相位的低通數
字濾波器。
- 如果Ha(s)是穩定的，即其極點在S左半平面，映射到H(Z)也是穩定的。
- 脈衝回響不變法的最大缺點：有頻譜周期延拓效應，因此只能用於帶限的頻響特性，如衰減特性很好的低通或帶通。而高頻衰減越大，頻響的混淆效應越小，至於高通和帶限濾波器,由於它們在高頻部分不衰減，因此將完全混淆在低頻回響中。所以用脈衝回響不變法實現高通和帶限濾波器時，應增加一保護濾波器，濾掉高於摺疊頻率以上的頻帶，然後再用脈衝回響不變法轉換為數字濾波器，這會增加設計的複雜性和濾波器的階數，只有在一定需要頻率線性關係或保持網路瞬態回響時才採用。
