基本介紹
- 中文名:翼型試驗
- 外文名:Airfoil test
- 學科:航空航天
- 類型:飛行術語
- 又稱:翼型風洞試驗
- 風洞試驗:確定飛行器氣動參數的重要途徑
試驗裝置
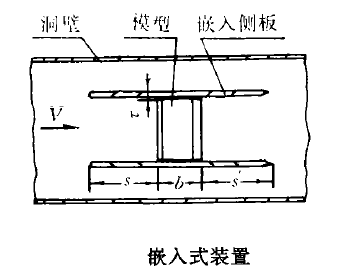
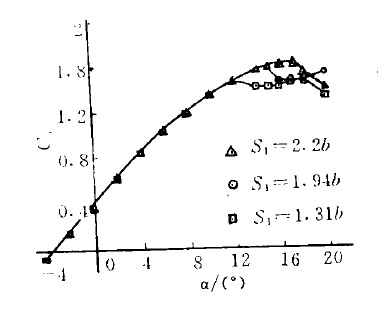



翼型試驗又稱翼型風洞試驗。流體力學方面的風洞實驗指在風洞中安置飛行器或其他物體模型,研究氣體流動及其與模型的相互作用,以了解實際飛行器或其他物體的空氣動力學特性的一種空氣動力實驗方法。為探討跨音速洞壁干擾效應,1981年...
翼型風洞又稱翼型風洞試驗,是針對翼型進行的風洞試驗研究。DU93-W-210翼型風洞試驗模型 實驗模型由角鋼骨架和玻璃鋼蒙皮組成。翼型內部設計有一空腔,空腔是由角鋼焊接成的框架,截面尺寸約為50 cm x 12 cm。空腔內間隔一定距離焊接加強...
《翼型氣動性能低速風洞測壓試驗要求》,是工業和信息化部批准2020年8月批准的行業標準。本標準規定了在低速風洞中進行翼型測壓試驗的一般要求、試驗程式與方法、數據採集與處理、試驗報告編寫和技術檔案交付與歸檔等要求。本標準適用於在...
二維模型試驗是指利用二維模型,在風洞中測量模型(如翼型)空氣動力特性的試驗。定義 二維模型試驗是指利用二維模型,在風洞中測量模型(如翼型)空氣動力特性的試驗。二維模型 二維模型,是一種較一維模型更完備的模型。對研究對象建立數學...
利用各種專門的試驗設備進行接近使用情況的數學和物理模擬試驗,用以考察和鑑定飛機飛行性能、使用性能和可靠性(見飛行器試驗)。風洞實驗 飛機風洞實驗分為:①空氣動力學的基礎性研究,如流場機理實驗等;②套用性研究,如翼型數據和外形...
在18世紀,羅賓斯(Robins)用旋臂機構使多種形狀的物體在空氣中運動,測量其空氣動力;18世紀末和19世紀初,凱利(Cayley)用旋臂機構系統地研究了翼型的升力和阻力。旋臂機構的主要缺點是試驗物體在其自己擾動的氣流尾跡中運動,於是人們...
NACA翼型是美國國家航空諮詢委員會(NACA)開發的一系列翼型。每個翼型的代號由“NACA”這四個字母與一串數字組成,將這串數字所描述的幾何參數代入特定方程中即可得到翼型的精確形狀。含義解釋 NACA四位數字翼型 是美國NACA最早建立的一個...
他當時的設計思想與20世紀30年代以來一直沿用的翼型曲線相去甚遠。經典翼型是上面較圓的弧形。人們認為,這樣能產生最大的升力。惠特科姆用了二年時間,對機翼的形狀進行了耐心的研究,並在風洞裡進行了幾周試驗。他發現,機翼頂面越是...
槽類量水建築物是一種灌區常見的特設量水設施,NACA翼型量水設施的經典翼面外形具有良好的流體動力特性,對其流場結構進行研究是討論其測流機理的關鍵。本項目基於模型試驗與數值仿真技術,通過討論不同工況下經典NACA翼型量水槽、量水柱的...
6.3.4 半模型試驗舉例及初步結論 6.4 模型表面壓力分布試驗 6.4.1 測壓模型的技術要求 6.4.2 試驗方法 6.4.3 數據處理 6.4.4 表面壓力分布測量的新方法 6.5 二維翼型試驗 6.5.1 試驗方法 6.5.2 側壁邊界層的影響...
4.1 全模測力試驗 4.1.1 飛機縱向氣動特性 4.1.2 飛機橫向氣動特性 4.1.3 飛機操縱面氣動特性 4.1.4 地面效應試驗”4.2 壓力分布試驗 4.2.1 測壓試驗方法 4.2.2 測壓試驗數據處理 4.3 翼型試驗 4.3...
5.3試驗裝置、方法及數據處理 5.3.1風洞 5.3.2模型安裝 5.3.3測試儀器 5.3.4試驗內容及數據處理 5.4試驗結果 5.4.1自由轉捩工況 5.4.2固定轉捩工況 5.4.3試驗結果與理論計算對比分析 5.4.4不同翼型風洞試驗結果對比 ...
自適應翼型亦稱變彎度翼型,它是一種有柔性的前緣和後緣,翼面為連續、光滑、沒有開縫或滑動接頭的機翼。該機翼的外形及彎度可根據任務需要而改變。自適應機翼的翼型由內部聯動裝置來控制,使其能隨飛行高度、Ma、後掠角和所需要的升力...
4.5幾類特種試驗的洞壁干擾問題138 4.5.1二元翼型試驗138 4.5.2半模型試驗141 4.5.3非定常試驗146 4.5.4V/STOL試驗148 4.6自適應壁技術151 參考文獻155 第5章支撐干擾試驗與修正方法159 5.1支撐干擾概述159 5.1.1模型...
試驗內容 隨著航空工業的日益發展,氣動彈性要求在飛機設計中的地位也越來越重要。薄翼型、全動平尾、垂尾、T形尾等設計構型的引入,增加了顫振發生的機率。為保證所設計的飛機具有氣動彈性穩定性,在對飛機進行周密的氣動彈性分析後,還...
在低雷諾數風洞對一種自行設計的柔性翼微型飛行器進行了國內首次垂直陣風試驗,並與翼型、機翼平面形狀和尺寸大小均相同的固定翼飛行器進行了性能對比。研究結果 為提高 MAV 的穩定性和抗風能力,進行了柔性翼微型飛行器的垂直陣風風洞試驗...
當飛機在空中飛行時,作用在飛機上的升力主要由機翼產生;同時機翼上也會產生阻力。機翼上的空氣動力的大小和方向很大程度上取決於機翼的外形,即機翼翼型、機翼平面幾何形狀等等,而翼展就是描述機翼平面幾何形狀的重要參數之一。相關研究 ...
④柔壁自適應風洞的邊界條件可控性好,可用來進行某些特殊目的的試驗,如地面效應試驗、翼柵流動試驗等。2、按可調節流動類型:分為二元自適應壁風洞和三元自適應壁風洞。二元自適應壁風洞僅有上下兩個壁面可以調節,對於翼型試驗,它可以...
2008年,加拿大麥吉爾(MiGill)大學的研究人員對帶有格尼襟翼的翼型在靜態和振盪運動中的空氣動力特性進行了風洞試驗探索研究。試驗中採用了NACA0012翼型,模型的展長為37.5厘米、弦長為15厘米,以及使用了8種不同形式的格尼襟翼,包括兩種...
(4)鉸鏈力矩試驗;(5)通氣模型試驗;(6)進氣道試驗;(7)噴流試驗;(8)動導數試驗;(9)壓力脈動試驗;(10)抖振試驗;(11)顫振試驗;(12)模型自由飛試驗;(13)空速管校準試驗;(14)二維翼型試驗;(15)流態及...
滑動蒙皮主要是讓機翼內部的縫隙最小,柔性蒙皮的設計就是使機翼在延伸和收縮時其上均有最小的壓痕,更具挑戰性的是可變翼需要其在任何時候均有最佳的翼型。控制 在控制方面可變形飛機有兩個挑戰是傳統飛機碰不到的。第一個挑戰是可...
1. 一種風洞試驗用三孔探針式測壓尾耙,發明專利(ZL201210146373.0),授權日:2014年07月16日,發明人:焦予秦、陳希平、解亞軍、竹朝霞、白靜、王鼎聖.2. 一種用於翼型風洞試驗的測壓尾耙,發明專利(ZL201210146288.4),授權日...
於是,有人開始研究能在飛行時改變機翼的後掠翼角度的飛機,起降和低速飛行時呈平直機翼,在高速飛行時呈後掠翼或三角翼型,較好地解決飛機低速和高速飛行性能的矛盾。早在笫二次世界大戰期間,德國就已進行了這項研究。美國戰勝並占領...
主要在以下四個方面獲得了一定研究成果: 1、自由表面影響下的對稱翼型機翼翼尖渦結構及氣動力特性 對稱機翼翼尖渦結構形態是整個研究項目的基礎,研究結果做為最基本的數據與非對稱及安裝了增生裝置的機翼試驗結果相對比。研究發現小攻角...
與此同時,由於考慮到了翼型的細節變化,附面層內的流場結構成為影響設計結果重要因素,此時傳統的依靠無黏流動的氣動分析手段已不再適用。為了彌補傳統戰鬥機機翼設計的不足,相關試驗研究了在跨音速/超音速巡航狀態下,小展弦比薄機翼的...
3.2.1 翼型流動試驗 3.2.2 理論與試驗對比分析 第4章 旋翼翼型設計理論與建模 4.1 概述 4.2 翼型氣動性能分析理論與建模 4.2.1 翼型氣動性能 4.2.2 空間離散 4.2.3 流場求解 4.2.4 多重格線求解加速 4.2.5 求解...
在有的機翼上,雖然各剖面翼弦在同一平面上(無幾何扭轉),但是沿展向採用了不同彎度的非對稱翼型。從空氣動力的角度來看,它實際上與幾何扭轉的作用相同,也起控制機翼展向升力分布的作用。這種情況稱為氣動扭轉。在實際機翼上,常見...
