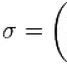置換的奇偶性

在數學中，當 X 是一個至少有兩個元素的有限集合時，X 的置換（即從 X 到 X 的雙射）可分為大小相同的兩類：奇置換與偶置換。

基本介紹

• 中文名：置換的奇偶性

性質

恆同置換是偶置換。一個偶置換可以由恆同置換通過偶數次兩個元素互換（稱為對換）得到，而一個奇置換可由奇數次對換得到。

由整數加法相應的法則馬上得到下列性質：

• 兩個偶置換的複合是偶的
  
• 兩個奇置換的複合是偶的
  
• 一個奇置換與偶置換的複合是奇的
  

由此得到

• 任何偶置換的逆是偶的
  
• 任何奇置換的逆是奇的
  

定理

置換的全體Sn的偶置換的全體構成一個階的子群，記作交錯群（交代群）。

例子

考慮集合 {1,2,3,4,5} 的置換 σ，它將初始排列 12345 變為 34521。可以通過三個對換得到：首先交換1和3的位置，然後交換2和4，最後交換1和5。這證明了給定的置換 σ 是奇的。