又稱纖維增強複合材料破壞理論,它們給出纖維增強複合材料因承受載荷而破壞時應力分量或應變分量應滿足的條件。
基本介紹
- 中文名:纖維增強複合材料破壞準則
- 外文名:failure criteria of fibre reinforced composites
簡介
分類
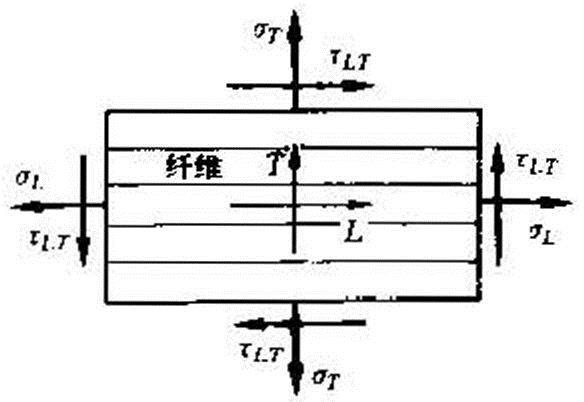 圖1 單向纖維板及其中的應力
圖1 單向纖維板及其中的應力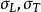
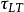
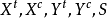
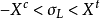
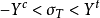
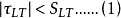
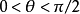
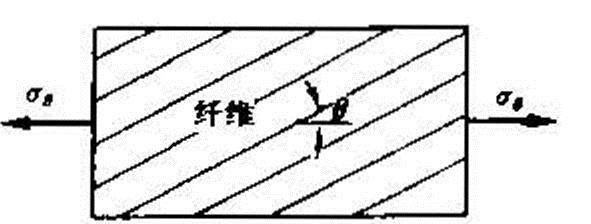 圖2 只在θ方向承受拉應力的單向纖維板
圖2 只在θ方向承受拉應力的單向纖維板
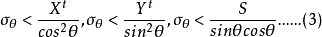

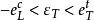


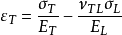
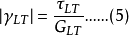
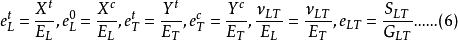


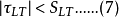
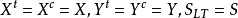
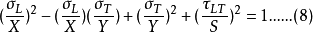
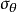
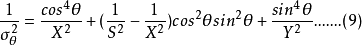
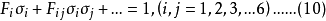
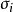

又稱纖維增強複合材料破壞理論,它們給出纖維增強複合材料因承受載荷而破壞時應力分量或應變分量應滿足的條件。
 圖1 單向纖維板及其中的應力
圖1 單向纖維板及其中的應力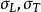
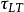
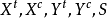
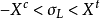
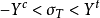
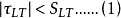
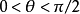
 圖2 只在θ方向承受拉應力的單向纖維板
圖2 只在θ方向承受拉應力的單向纖維板
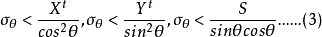

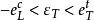


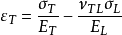
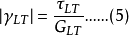
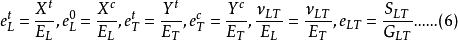


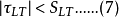
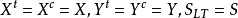
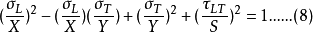
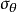
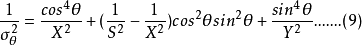
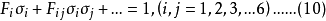
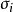

又稱纖維增強複合材料破壞理論,它們給出纖維增強複合材料因承受載荷而破壞時應力分量或應變分量應滿足的條件。...
《先進纖維增強複合材料性能測試》是2005年化學工業出版社出版的圖書,作者是J.M.霍奇金森。...
內容簡介本書為“斛兵博士文叢(2010)”中的一本,是在作者博士論文基礎上編寫而成的,該論文為合肥工業大學2010年優秀博士論文。 近年來,纖維增強複合材料FRP(Fiber...
第1章 複合材料概述1.1 纖維增強複合材料的分類1.2 複合材料的基本構造形式及...第5章 複合材料單層板強度理論5.1 線彈性體破壞準則的唯象理論5.2 正交各向...
近代複合材料最重要的有兩類:一類是纖維增強複合材料,主要是長纖維鋪層複合材料...1968年,經蔡為侖和希爾的多年研究形成了蔡-希爾破壞準則;後於1971年又出現了...
2.3.2最大應力強度準則和最大應變強度準則 2.3.3蔡—希爾(Tsai—Hill)強度...4.6.5 短切纖維氈增強複合材料的彈性常數和強度 4.7顆粒增強複合材料的彈性常...
樹脂基複合材料層壓板,是以樹脂為基體的複合材料層壓板、常用的樹脂有熱固性的不飽和聚醋、酚醛、氨基樹脂、環氧以及某些熱塑性樹脂;增強材料多為纖維及其織物,如...
2.4複合材料的力學性能複合準則2.4.1複合材料的剛度2.4.2複合材料的強度...5.4金屬基複合材料界面對性能的影響5.4.1連續纖維增強金屬基複合材料的低應力破壞...
在巨觀研究方面,美籍華人蔡為侖和R.希爾在50年代建立了各向異性複合材料的破壞準則;以後,又出現了蔡-吳張量破壞準則;近十餘年來在纖維增強複合材料的板殼力學方面...
2.5.3平面應力下單向複合材料的強度和破壞準則 2.5.4單向連續纖維增強複合材料力學性能的細觀分析 2.5.5單向複合材料的強度 2.6變動載荷(應力)和疲勞破壞的特性 ...
在巨觀研究方面,美籍華人蔡為侖和R.希爾在50年代建立了各向異性複合材料的破壞準則;以後,又出現了蔡-吳張量破壞準則;近十餘年來在纖維增強複合材料的板殼力學方面...
