縱向數據作為一種特殊形式的數據,廣泛地產生於醫學和社會學等領域。它主要來自於是每個個體在不同時間點上的觀測值。
基本介紹
- 中文名:縱向數據處理
- 外文名:vertical data-processing
- 別稱:縱向數據分析
- 傳統處理:重複測量方差、時間序列分析
- 新型處理:潛變數增長曲線模型、多層線性等
- 套用學科:計算機科學、建築科學、心理學
簡介,傳統縱向數據分析方法,重複測量方差分析,時間序列分析,新型縱向數據處理方法,潛變數增長曲線模型,多層線性模型,縱向數據處理方法述評,套用前景,
簡介
縱向數據作為一種特殊形式的數據,廣泛地產生於醫學和社會學等領域。它主要來自於是每個個體在不同時間點上的觀測值。參數混合模型(也叫隨機效應模型)是分析縱向數據的有力工具。縱向數據研究的一個難點是怎樣考慮組內相關,而線性和非線性混合效應模型很好地解決了這個問題,所以線性和非線性混合效應模型被廣泛的套用於縱向數據的研究。
傳統縱向數據分析方法
重複測量方差分析
重複測量的方差分析在實際中有非常廣泛的套用,其中的一個作用就是用來分析重複測量實驗設計(又稱被試內設計,混合設計等)得來的數據。該方法通過把總的變異分解為被試內和被試間兩部分,對被試的平均增長趨勢進行分析,可以通過多項式比較分析線性增長趨勢和非線性增長趨勢。如果研究中我們只關心不同時間點的平均數間是否存在差異可,以用單變數方差分析解決這一問題。但是值得注意的是,套用重複測量的方差分析時,必須滿足協方差矩陣球形sphericity的假設條件,也就是說,MANOVA要求所有重複測量的總體的方差相等並且所有重複測量總體之間的協方差也相等。如這一條件不滿足,那么得到的F檢驗統計量的值正偏,拒絕虛無假設的機率增大,也就是說如果觀測變數協方差矩陣球形假設條件不滿足,傳統重複測量的方差分析的統計檢驗力降低,F檢驗犯第一類錯誤的機率增大。另外,MANOVA不能用來處理依時間變化的協變數對因變數的影響。關於重複測量方差分析的詳細介紹在大多數的統計資料中都有較詳細的介紹。
時間序列分析
時間序列分析是對縱向研究數據進行分析的另外一類非常重要的統計分析技術。它在許多領域都有十分重要的套用,尤其在預測和控制套用方面有著其它方法不可比擬的優點。時間序列分析以回歸分析為基礎,目的在於測定時間序列中存在的長期趨勢、季節性變動、循環波動及不規則變動並進行統計預測。
為了對時間序列中不同的變化趨勢進行分析,主要有兩大類模型經典模型:KineticModel和動態模型。DynamicalModel經典模型是將時間序列{xt,t∈T}看作是時間的函式xt=f(t);而動態模型是將t時刻的觀測看成是t時刻前觀測值,可以與t時刻的觀測類型相同也可以不同的函式,xt=f(xt-1,xt-2...)
通常所說的AR,ARMA,ARMIA模型都屬於這一類。為了便於和其他幾種方法比較,只簡單介紹第一種類型模型。對於第一種類型的模型,常用的模型有加法模型,即假定各構成部分對時間序列的影響是相互獨立的。這時可以將時間序列表示為xt=T+C+S+I,其中T、S、C、I分別代表時間
時間序列中存在的長期趨勢、季節性變動、循環波動及不規則變動;另一類是乘法模型,即假設各組成部分對時間序列的影響均按比例變化,從而可以把時間序列表示為xt=T×C×S×I。除上面的加法模型和乘法模型外,還有其它混合模型,不再一一列舉。進行時間序列分析,如果要測定長期趨勢,可以是直線的,也可以是非直線的,可以通過移動平均法時、距擴大法或數學模型法,剔除時間序列中循環波動C、季節性變動S及不規則變動I,使得時間序列的長期增長趨勢顯現出來,對於時間序列中的第二類模型在實際中有許多套用模型,分類也比較複雜,需要對時間序列的平穩性進行分析,並且要求研究者有較高的數學素養。另外由於時間序列分析往往要求較多的連續觀測時間點,所以在心理學和教育學中用的不是很多。
新型縱向數據處理方法
潛變數增長曲線模型
潛變數增長曲線模型是用於固定情形(fixedoccasion)縱向研究數據的一種統計分析方法,也就是說,該方法適用於在某幾個固定時間點觀測得來的縱向研究資料。在潛變數增長曲線模型中,用潛變數來描述總體的平均增長趨勢和依時間變化的情況。基本模型可以用下圖表示(圖): 潛變數增長模型結構圖
潛變數增長模型結構圖
 潛變數增長模型結構圖
潛變數增長模型結構圖圖描述的是含有五個測試時間點的潛變數增長模型,Y1i,Y2i,Y3i,Y4i,Y5i分別表示第i個被試的5次測量結果,上述模型可以表示為:

其中π0i,π1i分別表示截距和斜率,在上面的模型中,這一截距和斜率為隨機參數,(2)和(3)進一步解釋上述截距π0i和斜率π1i的變化。
從上面模型的描述可以看出潛變數增長曲線模型同時考慮因素的平均值和方差,也就是說,潛變數增長曲線模型不僅分析了總體的發展趨勢,而且可以分析總體之間存在的差異。
事實上,在上述的潛變數模型中,只是簡單地定義了線性增長模型,在實際中,可以不固定斜率測量的因素載荷(如在圖中讓固定為2,3,4的斜率載荷自由估計)得到增長曲線模型,還可以定義測量誤差之間的不同關係(如限定測量誤差相等,誤差間存在一階自相關,二階自相關等等)。有關潛變數增長曲線的更詳細的和深入的介紹,可以參看Duncan的著作。
潛變數增長曲線模型可以用協方差結構模型(SEM)軟體進行分析,常用的軟體有Lisrelt,AMOS,EQS和MPLUS等。
多層線性模型
多層線性模型是用於分析具有嵌套結構特點數據的一種統計分析技術,近年來在教育、管理等領域有相當廣泛的套用。當對相同的觀測對象進行重複測量時,可以將這些重複測量的數據本身看成是具有嵌套結構特點的。如對生長發育期兒童身高和體重變化情況的追蹤調查等,可將這些重複測量數據構造出一個兩水平的層次結構,其重複測量或測量點為水平1的單位,觀測個體為水平2的單位,這時就可用多層分析的方法對縱向數據進行分析。
對於重複測量的數據,用層次分析法描述數據之間的關係,對應的兩水平重複測量模型,可以用下式表示(下面只給出最簡單的一種多層模型形式,實際上,可以進一步考慮更多的不同水平預測變數和更複雜的隨機殘差之間的關係):
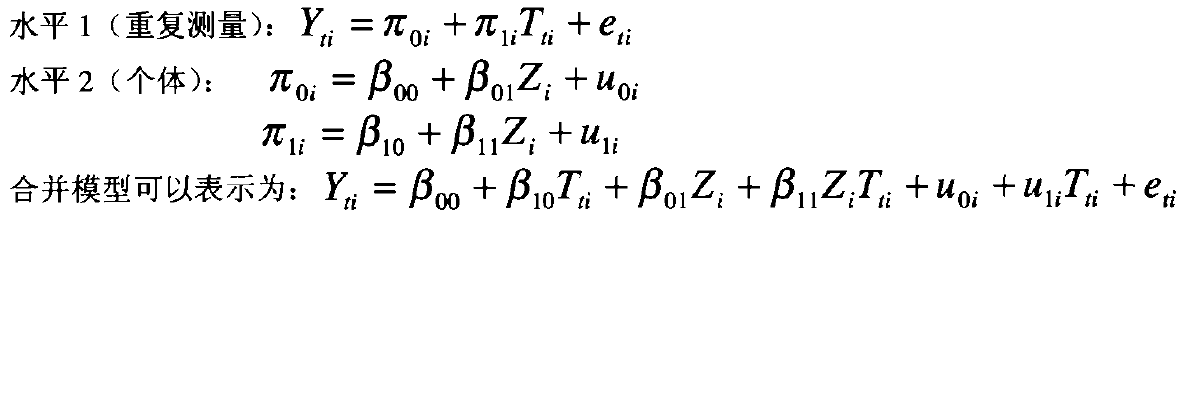
從上面的模型中可以看出,與潛變數增長曲線模型類似,多層分析不僅可以分析總體上個體隨時間的變化(截距β00和斜率β00,而且可以將個體之間增長的差異進行分析(截距的差異u0i,斜率的差異u1i),並將這一差異的原因進行解釋(β00解釋截距的差異和β00解釋斜率的差異)。
可以在上述模型中包含更多的水平I的隨機誤差。這主要是由於在重複測量的模型,測量與測量之間往往是相關的而不是獨立的(如在個體水平上的多次測量,由於具有相同的個體特徵和測量間的相互影響,存在的測量誤差(第一水平的隨機誤差)之間的“自相關”。
對於多層線性模型的數據分析,可以採用專門的軟體進行分析,常用的用於多層分析的統計分析軟體有:HLM,MLn,VARCL,SAS和Mplus。
縱向數據處理方法述評
上面介紹的用於縱向研究的常用方法,各有優缺點,簡述如下:
重複測量的方差分析主要用來比較均值間的差異,一般不對增長的變異情況進行分析,也就是說,重複測量的方差分析主要用來描述總體的平均增長趨勢,而不關注個體增長曲線存在的差異,有計算簡單,易於理解等優點。最主要的缺點是不能就個體之間存在差異的原因進行分析和解釋,數據中的缺失值不能得到精確的估計,在數據缺失量較大時,分析所用數據信息損失較大。另外,重複測量方差分析不能處理分段間距不等或測量次數不等的數據。
時間序列分析是一類很有用的分析數據隨時間變化趨勢的統計技術,在自然科學和社會科學各個領域都有非常重要的套用價值,但是由於其理論比較複雜、要求測試的時間點相對具有連續性和要求較多的測試時間點等特點,所以在心理學和教育學的研究中用的不是特別普遍。
採用多層分析的方法處理重複測量數據與時間變數之間的關係,在多層結構中,可以對非平衡測量數
據得到參數的有效估計,因此用多層分析法處理重複測量的數據,不要求所有的觀測個體有相同的觀測數,在縱向調查研究中,由於各種各樣的原因,被試個體觀測值部分缺失的情況時有發生,因此多層分析法處理缺失數據而不影響參數估計精度的這一特徵,使得多層分析法處理在處理縱向觀測數據時,比傳統多元重複測量方法有很大的優勢。與傳統的用於處理多元重複測量數據的方差分析和回歸分析方法相比,多層分析法至少具有以下優點:多層分析法通過考慮測量水平和個體水平不同的差異,明確表示出個體
在水平1(不同測量點)的變化情況,因而對於數據的解釋(個體隨時間的增長趨勢)是在個體與重複測量互動作用基礎上的解釋,即不僅包含了不同測量點的差異,而且包含了個體之間存在的差異;多層分析法對數據資料較傳統多元重複測量方法有較低的要求,對於重複測量的次數和重複測量之間的時間跨度都沒有嚴格的限制,不同個體可以有不同的測量次數,測量與測量之間的時間跨度也可以不同;多層分析模型可以定義重複觀測變數之問複雜的協方差結構,並且對所定義的不同的協方差結構進行顯著性檢驗,在多層分析模型中,通過定義第一水平和第二水平的隨機變異來解釋個體隨時間的複雜變化情況;當數據滿足傳統多變數重複測量模型對數據的要求和假設時,層次分析法得到與傳統固定效應多元重複測量模型相同的參數估計和假設檢驗結果;用多層分析模型可以考慮更高一層的變數(如不同地區兒童)對個體增長的影響。但是多層分析模型也有缺點,首先用於多層分析模型的參數估計方法較傳統估計參數的方法要複雜得多,而且與後面介紹的LGM方法相比也不能處理變數之間間接的影響關係和處理複雜的觀測變數和潛變數之間的關係。
潛變數增長曲線模型(LGM)可以直接處理變數之間複雜的因果關係,即不僅可以對變數之間直接的影響關係進行分析,而且可以將變數之間間接的因果關係進行分析;另外,由於潛變數結構模型是基於協方差結構模型的理論,所以不僅可以分析觀測變數之間的關係,而且可以在考慮測量誤差的基礎上對潛變數之間的因果關係進行考察;上面介紹的多層分析模型只能分析變數之間的直接因果路徑,對於潛變數之間關係的分析要比LGM複雜得多,並且在測量模型上也有更多的限定條件。LGM模型可以簡便地處理變數測量誤差(殘差)之間的關係,而不必限定殘差之間相互獨立,如可以直接定義類似於AR和ARMA模型中所要求的殘差之間的關係類型;用HLM雖然沒有殘差之間相互獨立的要求,但是用現有的多層分析軟體定義起來要比LGM複雜得多。LGM的另外一個優點是,因為LGM分析可以採用標準的用於SEM的分析軟體,所以可以得到模型整個擬合的情況,並且可以根據提供的修正指數對模型進行修改。LGM不僅就個體的發展軌跡進行描述,而且可以分析個體之間存在的差異以及存在差異的原因;LGM不僅可以對給定的增長趨勢進行檢驗,而且在觀測時間點多於兩點的情況下可以對個體隨時間變化的趨勢類型(如直線或曲線)進行探索。LGM可以分析依時間變化的預測變數對因變數的影響,並且可以用類似於SEM中多樣本比較的方法對多個樣本之間的差異進行檢驗,可以有效處理缺失值。但是LGM也有如下缺點,因為LGM用SEM的基本原理對變數之間的關係進行分析,所以為了得到可靠的分析和檢驗結果,往往要求比較大的樣本容量:對於所有個體的評估要求測試時間間隔相同,如果個體的變化隨時間變化趨勢不是很明顯,LGM方法與傳統方法相比沒有明顯的優勢。
套用前景
在心理學套用中,對於縱向研究的資料,我們往往不僅對個體增長的平均趨勢感興趣,而且希望分析個體之間增長存在的差異。作為綜合分析方法,應當能夠同時解決這兩個問題。潛變數增長曲線模型和多層分析模型是在傳統分析方法基礎上發展起來的綜合分析的統計技術,這兩種方法可以同時解決上面提到的兩個問題。從國外縱向研究的發展趨勢來看,這兩種方法近年來越來越受到重視,其原因不僅是因為這兩種方法是一種新的統計分析技術,更重要的是他們可以幫助我們發現事物發展的更深一層的規律,可以對個體之間的發展變化進行進一步的分析和解釋,為理論研究提供更加有意義的實證研究的成果。國內心理學研究中,多層分析方法處於起步階段,潛變數增長曲線模型還沒有見有介紹。
在心理學研究中,人們已經不滿足於現象的描述(橫斷數據資料的分析)和簡單的差異的檢驗,要對人類心理現象發展的內在心理機制進行研究,把握事物發展的內在規律,縱向研究必然越來越受到研究者們的重視。隨著縱向研究方法的套用,用於縱向數據分析的綜合統計分析技術——潛變數增長曲線模型和多層分析法必然受到研究者們的青睞。

