線性二次控制（Linear quadratic control）是指線性的，性能指標泛函是狀態變數和控制變數的二次型函式的積分，並且由狀態變數構成線性狀態反饋方式。
基本介紹
簡介,二次型,簡介,二次型函式的定義,線性控制理論,簡介,理論研究對象,線性二次型最優控制,二次型性能指標,狀態調節器問題,
簡介
線性二次控制（Linear quadratic control）是指線性的，性能指標泛函是狀態變數和控制變數的二次型函式的積分，並且由狀態變數構成線性狀態反饋方式。
如果系統是線性的，性能指標泛函是狀態變數和控制變數的二次型函式的積分，並且由狀態變數構成線性狀態反饋系統，則這樣的最優控制稱為線性二次最優控制。以下介紹的是線性二次型最優控制的基本知識。首先介紹了二次性能指標，然後討論了調節器問題。
二次型
簡介
二次型，quadratic form。n個變數的二次多項式稱為二次型，即在一個多項式中，未知數的個數為任意多個，但每一項的次數都為2的多項式。線性代數的重要內容之一，它起源於幾何學中二次曲線方程和二次曲面方程化為標準形問題的研究。二次型理論與域的特徵有關。
二次型函式的定義
定義設z是n維列向量，稱標量函式
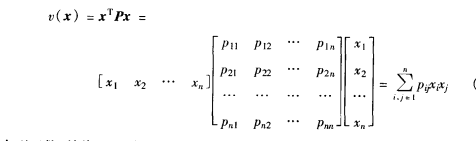
圖1
為二次型函式，並將P稱為二次型的矩陣。上式是二次型函式的矩陣表達式，該式又可展開為
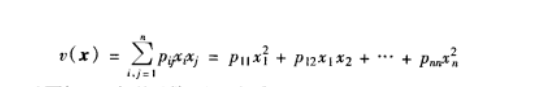
圖2
由式2可知，二次型函式v( x)實質上是關於xi和xj的二次多項式。由於多項式中，同類項合併後可再平分係數，因此可以整理成對稱係數。也就是說，一個二次型函式總可以化成二次型矩陣P為實對稱矩陣的二次型函式。
線性控制理論
簡介
線性控制理論是系統與控制理論中最為成熟和最為基礎的一個組成分支，是現代控制理論的基石。
系統與控制理論的其他分支，都不同程度地受到線性控制理論的概念、方法和結果的影響和推動。
系統是由相互關聯和相互作用的若干組成部分按一定規律組合而成的具有特定功能的整體。系統可具有完全不同的屬性，如工程系統、生物系統、經濟系統、社會系統等。但是，在系統理論中，常常抽去具體系統的物理或社會含義而把它抽象化為一個一般意義下的系統而加以研究，這種處理方法有助於揭示系統的一般特性。
系統最基本的特徵是它的整體性，系統的行為和性能是由其整體所決定的，系統可以具有其組成部分所沒有的功能，有著相同組成部分但它們的關聯和作用關係不同的兩個系統可呈現出很不相同的行為和功能。
理論研究對象
線性系統理論的研究對象為線性系統，它是實際系統的一類理想化了的模型，通常可以用線性的微分方程和差分方程來描述。
在系統與控制理論中，我們將主要研究動態系統，通常也稱其為動力學系統。動態系統常可用一組微分方程或差分方程來表征，並且可對系統的運動和各種性質給出嚴格和定量的數學描述。當描述動態系統的數學方程具有線性屬性時，稱相應的系統為線性系統。線性系統是一類最簡單且研究得最多的動態系統。
線性二次型最優控制
如果系統是線性的，性能指標泛函是狀態變數和控制變數的二次型函式的積分，並且由狀態變數構成線性狀態反饋系統，則這樣的最優控制稱為線性二次最優控制。以下介紹的是線性二次型最優控制的基本知識。首先介紹了二次性能指標，然後討論了調節器問題。
二次型性能指標
二次型性能指標的一般形式如下
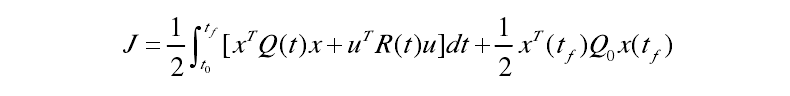
圖3
式中
- Q(t)一一nxn維半正定的狀態加權矩陣;
- R(t)一一rxr維正定的控制加權矩陣;
- Qo一一nxn維半正定的終端加權矩陣。
在工程實際中，Q(t)和R(t)常取對角陣。
下面對性能指標中各項的物理意義作逐一解析。
被積函式中第二項
，表示動態過程中對控制的約束或要求，如
果把u看成電壓或電流的話，那么Lu與功率成正比，而
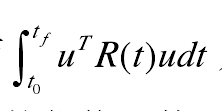
圖4
表示在
區間內消耗的能量，因此，Lu是衡量控制功率大小的代價函式。
式中第二項突出了對終端誤差的要求，叫做終端代價函式。例如在宇航的交會問題中，由於要求兩個飛行體終態完全一致，因此，必須加上這一項，以體現tf時誤差足夠的小，至於Qo ， R(t)的加權意義和Q(t)相仿。
如果最優控制的目的是使J →min，則其實際意義在於用不大的控制，來保持較小的誤差，從而達到能量和誤差綜合指標的最優的目的。
狀態調節器問題
狀態調節器的任務是，當系統狀態由於任何原因偏離了平衡狀態時，能在不消耗過多能量的情況下，保持系統狀態各分量仍然接近於平衡狀態。在研究這類問題時通常把初始狀態矢量看成擾動，而把零狀態取做平衡狀態。於是調節器問題就變為尋找最優控制規律“，在有限的時間區間[fto } tf」內，將系統從初始狀態轉移到零點附近，並使給定的性能指標泛函取極值。
設線性時變系統的狀態空間表述為
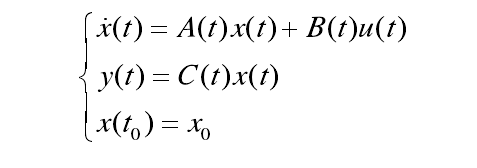
圖5
- x, u, y一一分別為n, r, m維矢量;
- A(t)一一hxh維系統矩陣;
- B(t)一一hxr維輸入矩陣;
- C(t)一一mxh維輸出矩陣;
性能指標泛函如圖5所示
下面給出狀態調節器的解最優控制器為
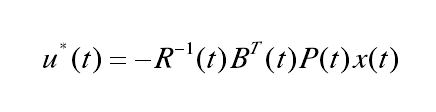
圖6
最優性能指標為
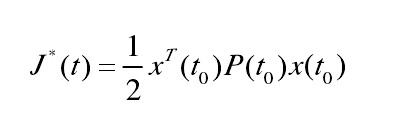
圖7
式中P(t)滿足下面的Riccati矩陣微分方程
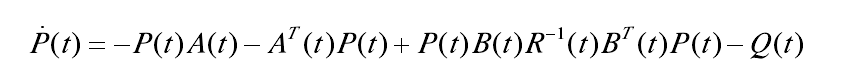
與8
邊界條件
