經驗風險最小化(ERM)是統計學習理論中的一個原則,它定義了一系列學習算法,並用於給出其性能的理論界限。
基本介紹
- 中文名:經驗風險最小化
- 外文名:Empirical risk minimization
- 縮寫:ERM
介紹
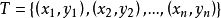

策略



經驗風險最小化(ERM)是統計學習理論中的一個原則,它定義了一系列學習算法,並用於給出其性能的理論界限。
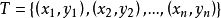




經驗風險最小化(ERM)是統計學習理論中的一個原則,它定義了一系列學習算法,並用於給出其性能的理論界限。...
結構風險最小化(Structural Risk Minimization)是指把函式集構造為一個函式子集序列,使各個子集按照VC維的大小排列;在每個子集中尋找最小經驗風險,在子集間折中...
在統計學習理論中,結構風險定義為經驗風險與置信風險的和。因為在機器學習理論中,雖然經驗風險最小化的歸納原則是一致的,但是一致性是在樣本數量趨向無窮大時得到了...
最大似然估計其實是經驗風險最小化的一個例子,而最大後驗估計是結構風險最小化的一個例子。如果樣本數據足夠大,最大後驗機率和最大似然估計趨向於一致,如果樣本...
1 背景 2 經驗風險最小化 3 主動式學習 有監督訓練背景 編輯 有監督訓練有兩種形態的模型。最一般的,監督式學習產生一個全域模型,會將輸入物件對應到預期輸出...
13 2 2經驗風險最小化(286)13 2 3複雜性與推廣能力(287)13 3統計學習理論的核心內容(288)13 3 1學習過程一致性的條件(288)...
1.5 經驗風險最小化歸納原則1.6 學習理論的四個部分非正式推導和評述——11.7 解決學習問題的傳統模式1.7.1 密度估計問題(最大似然方法)...
統計學習理論是研究利用經驗數據進行機器學習的一種一般理論,屬於計算機科學、模式...第5章 實損失函式風險的界 第6章 結構風險最小化原則 第6章附錄 基於間接測量...
17.3 經驗風險最小化原則的一致性條件 17.4 最優指示函式判決風險的界 17.5 訓練序列的長度和識別率估計精度的關係 17.6 結構風險最小化 文獻簡評 應...
3.1.6 核函式定義 633.2 風險控制策略 653.2.1 VC維概念 653.2.2 經驗風險最小化原則 663.2.3 結構風險最小化原則 673.3 樣本被錯分的討論 68...
5.6.2二維數據圖形化 5.6.3三維數據圖形化 5.6.4高維數據圖形化 第6章統計學習方法 6.1風險最小化問題 6.1.1經驗風險最小化 6.1.2結構風險最小...
12.1.2 經驗風險最小化原則12.1.3 複雜性與推廣能力12.2 統計學習理論12.2.1 VC維12.2.2 推廣性的界12.2.3 結構風險最小化原則12.3 支持向量機...
3.2.2經驗風險最小化 723.2.3複雜性與泛化性能 733.3統計學習理論的核心內容 743.3.1學習過程一致性的條件 753.3.2函式集的學習性能及VC維理論 76...
一、經驗風險最小化(EmpiricalRiskMinimization)二、結構風險最小化(StructuralRiskMinimization)三、構造支持向量機第二節支持向量機在農產品無損檢測中的套用...
表示,線上性可分問題下,硬邊界SVM的經驗風險可以歸0,因此其是一個完全最小化結構風險的分類器;線上性不可分問題中,軟邊界SVM的經驗風險不可歸0,因此其是一個...
1.1.2 經驗風險最小化 51.2 統計學習理論的產生 51.3 學習過程的一致性條件 71.4 VC維理論 81.5 推廣性的界 91.6 結構風險最小化 10...
軍事等多個學科領域的最熱門新興技術之一,具有寬泛的理論基礎和廣闊的套用前景。...16.4 經驗風險最小化41016.4.1 前向S形網路41116.4.2 矢量空間方法(...
3.1.4 經驗風險最小化原則3.1.5 複雜性和推廣能力3.1.6 模式識別問題3.2 統計學習理論的四個部分3.2.1 學習過程的一致性3.2.2 學習過程收斂速度的界3.2...
[-1, 1]線性生成運算元的數據無量綱化處理方法和基於煤炭產量的關聯度加權的兩種...1.2.2 經驗風險最小化原則 (7)1.2.3 VC維 (9)1.2.4 結構風險最小...
1. SVM 基於結構風險最小化原則構建學習機,RVM基於貝葉斯框架構建學習機...在SVM中懲罰因子是平衡經驗風險和置信區間的一個常數,實驗結果對該數據十分敏感,...
神經網路是一種非線性識別能力強的機器學習算法,是基於經驗風驗最小化原理的大...基於結構風險最小化原理,較好地解決小樣本、非線性和高維數難題,在交通、網路...
基於統計學習理論的VC維理論以及結構風險最小原理,支持向量機(CSVM)方法在提高學習泛化能力的同時,可實現置信範圍以及經驗風險最小化的目標。理論上解決了神經網路...
