基本介紹
內容簡介,基本模型,統籌模型,廣義模型,
內容簡介
統籌學，研究如何在實現整體目標的全過程中施行統籌管理的有關理論、模型、方法和手段，是數學與社會科學交叉的一個學科分支。統籌，英文為Overall planning，簡寫為OP。它通過對整體目標的分析，選擇適當的模型來描述整體的各部分之間，各部分與整體之間及它們與外部之間的關係和相應的評審指標體系，然后綜合成一個整體模型，用以進行分析並求出全局的最優決策以及與之協調的各部分的目標和決策。統籌學的理論與方法滲透到管理的許多領域。在安全管理中也有著重要套用。
統籌學
統籌學基本模型
統籌方法中的基本模型，是統籌圖(網路圖)。它是用節點、箭頭和與之相應的數來描述整體和各部分、各部分之間以及它們和外界之間的關係。從基本模型出發，根據不同的整體目標，還需選取與之相適應的其他模型。
當整體目標為完工時間的情形，可用箭頭表示各部分的內容，稱之為活動；節點表示事件，如某些活動完成，某些活動開始等；與箭桿相應的數字表示完成該活動所需的時間等；箭頭之間的銜接關係表示各部分之間的順序關係。從統籌圖的起點出發，沿著箭頭方向走到表示整體工作完成的節點（結束點），可以有一條或多條路線。其中花費時間最多者稱作主要矛盾線或關鍵路線，關鍵路線上的各活動稱為關鍵活動。關鍵路線可能不止一條，但是任一條關鍵路線所用的時間均相同，等於整體工作最早可能完工時間。據此，還可算出為保證整體完工的時間各活動的最遲必須開工時刻和最遲必須完工時刻、各活動的最早可能開工時刻和最早可能完工時刻。每個活動的最遲必須完工時刻與最早可能完工時刻之差稱為該活動的總時差。
統籌學模型
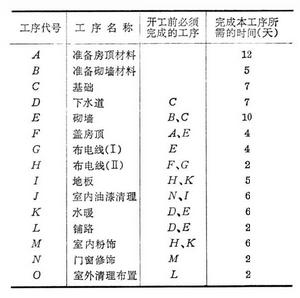
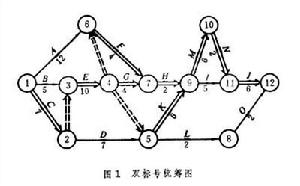
統籌學模型以建造一幢房子的工程為例，如果該工程的各部分活動（工序）經簡化後如表所列，則可以用雙標號統籌圖（圖1）來描述這項工程：
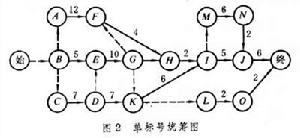
以兩個節點(i,j)表示一項活動，例如(3,4)表示活動E（砌牆）。節點的編號可以是任意的,習慣上常常選取編號使得對任一活動(i,j)都有i<j。也可以用一個節點表示一項活動，畫成單標號統籌圖（圖2）。
統籌學模型
統籌學模型圖1的關鍵活動用雙線表示。共有三條由點1到點 12的關鍵路線。每條關鍵路線都需要37天。在工程實施時，任何一個關鍵活動的延誤都可能拖延整體工作的完成時間。
如果整體工作所包含的活動很多很複雜，有關參數可以借電子計算機的幫助計算出來。假定統籌圖(圖1)上節點編號為1,2,…,n;tij為活動(i,j)所需的時間。如果活動(i,j)出現在統籌圖上,稱i為j的緊前節點，稱j為i的緊後節點,記B(j)為節點j的所有緊前節點的集合，A(i)為i的所有緊後節點的集合,那么節點j的最早可能開始時刻tE(j)可用如下的疊代公式算出： 設節點n的A(n)為空集,則T=tE(n)便是關鍵路線所需的時間。為保證整體工作的完成時間、節點 i的最遲必須完成時刻tL(i)可由類似公式疊代求出：
計算公式
計算公式活動(i,j)的最早可能開工時刻,最遲必須完工時刻，最遲必須開工時刻，最早可能完工時刻分別為：
統籌模型
(1)時間—成本最佳化模型。整體目標涉及時間與成本時，在統籌圖中與箭頭相應的數字表示時間與成本的關係。
(2)時間—資源最佳化模型。整體目標涉及時間與資源時，則可在工期一定的條件下，均衡不同時期資源需要量和相應各部分的有關參數。
(3)決策型模型。在決策階段面臨各部分多種方案的選擇，從整體出發，選擇其中之一方案。此時統籌圖上含有若干決策點。 (4)控制模型。在計畫實施階段，用以對財務、進度、資源等的控制。
(6)非肯定型統籌模型。與各部分相應的“給定數”是隨機向量。
為了更客觀地描述現實世界中存在的複雜的銜接關係和數量關係，還可引進廣義統籌模型，其中節點由前後兩部分組成，刻畫到達與離開此節點時的各部分之間的關係。
用節點和箭頭組成的統籌圖稱為決策型統籌圖，是進行多階段決策的有力工具。為找出總體最優解和與之相協調的各部分的指標和參數組，可按以下步驟分析廣義統籌圖。
①進行調查研究，畫出廣義統籌圖。②計算整體指標，計算方法有代數分析法、流圖計算法，矩母函式與W函式法；③評審與最佳化。根據綜合的整體指標，進行評審，找出現存整體的最優解，或對整體進行設計，以取得最優效果。④確定與整體協調的各項決策、各部分的指標與有關參數。⑤控制、調整與整理。
統籌學是管理科學中較為活躍的分支，它的套用範圍與效果隨計算機的發展而不斷擴大，並與數學的有關分支和社會經濟學結合產生一些新的有生命力的管理科學分支，進一步推動了統籌學的發展。
廣義模型
為了更客觀地描述現實世界中所存在的複雜的銜接關係和數量關係，引入了廣義統籌模型(GAN)。其中的節點由前後兩半部組成,刻畫到達與離開此節點的各部分之間的關係。節點兩半部的符號表示和含義如表所示。 它們分別組合成六類不同的節點(見圖)。圖中a是基本統籌圖中的節點；b表示 A1或A2有一個完成後，B1與B2皆執行；c表示當A1與A2中有一個且只有一個完成後, B1和B2皆執行；d表示A1與A2都完成後,決定B1執行或B2執行,或各以某種機率執行；e表示A1或A2有一個完成後，決定B1執行或B2執行,或按各自的機率執行；f表示A1、A2中有一個且只有一個完成後，決定B1執行或B2執行，或按各自的機率執行。在每個節點後代表各部分的每個箭頭，除時間參數外，還應有一數量表示執行該部分的機率, 如果肯定執行，機率為1。與箭頭相應的參數除時間外,還可以表示費用、收益、可靠性、信息量等等。
計算公式
計算公式用以上節點和箭頭組成的統籌圖稱為決策型統籌圖(決策型網路圖)，它是進行多階段決策的有力工具，決策樹則是其中較簡單的情形。進一步，如果圖上與各箭頭相應的參數向量（執行機率、時間、資源、可靠性、信息量等等）中有若干分量是隨機變數，稱為隨機型統籌圖(GERT)。
為了找出總體最優解和與之相協調的各部分的指標與參數組，可按下述步驟對廣義統籌圖進行綜合分析。
① 進行調查研究，畫出廣義統籌圖。
③ 評審與最佳化。根據綜合的整體指標，進行方案的評審,找出現存整體的最優解，或對整體進行設計,以達到最優效果。
④ 確定與整體協調的各項決策、各部分的指標與有關參數。
⑤ 控制、調整和整理。
對於隨機型的統籌模型，在計算總體綜合指標和尋找最優解時產生很大困難，因而又引入了一些求滿意解(但不一定是最優解)的方法。例如統籌模擬模型(GERTS)，將已建立的隨機型統籌圖利用計算機進行模擬，計算出整體綜合指標，或求出滿意解。
統籌學相關圖書
統籌學相關圖書