【概述】
組合推導法，來源於湖南攸縣第一中學洪開科老師發表在《數學學習與研究》雜誌 2015年01期的論文：教本探源求二項展開式的某項或某項的係數——談組合推導法的套用。
“組合推導法”是組合計數推導法的簡稱，這是偉大的物理學家數學家牛頓在1665年推導二項式定理方法，多項式的乘法本質是其結果由每個括弧中取一項相乘的所有單項式合併同類項得到的。求二項展開式的某項或某項的係數是高考數學的一個基本知識點，每年的高考題都有一定的題目出現，人們往往利用二項式定理的通項公式去解決，卻忽視了推導二項式定理的原理“組合推導法”，套用組合推導法比套用通項公式又快又好，可以起到事半功倍的效果。
基本介紹
- 中文名：組合推導法
- 外文名：Combination derivation method
原理,套用,
原理
教材中二項式定理的推導就是將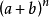
看成n個a+b相乘，從每個括弧中取一項（非a即b）相乘的所有單項式合併同類項得到的，按取b的個數分為n+1類，不取b的是
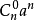；取1個b的是
，…，取r個b的是
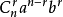，…，取n個b的是
，這就是組合推導法。理解了這個方法二項式定理就可信手拈來了，也可按取a的個數分為n+1類寫出來。
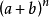
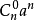
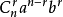
套用組合推導法求二項展開式的某項或某項的係數要注意三點：
第一是選取性，二項式的兩項怎樣選取（各取幾個）才能構成所求的項。
第二是有序性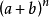， 的展開式第r+1項是取r個b（同時取n-r個a），這裡的a、b不能互換。
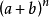
第三是項、項的係數與二項式係數的區別，某項要把這一項全部寫出來，某項的係數只寫這一項的係數不要帶字母（即把每個字母當作數1），某項的二項式係數就是相應的組合數
。
套用
一、直接求二項展開式的某項或某項的係數.
1．(2014年高考湖南卷)
的展開式中
的係數是( )
A．－20 B．－5 C．5 D．20
解析：依題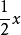
要取2個，故 的係數為
= -20，故選A.
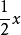
2．(2014年高考全國大綱卷)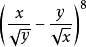
的展開式中
的係數是 ______(用數字作答).
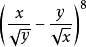
解析：依題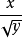
要取4個，故 係數是
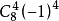=70.
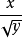
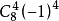
3．(2010年高考四川卷)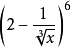
的展開式中的第四項是________ .
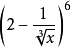
解析：依題
要取3個，故第四項是T4=
4．(2014年高考四川卷) 在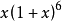
的展開式中，含
的項係數為( ).
A．30 B．20 C．15 D．10
解析：依題
中x要取2個，故 的係數為
=15，故選C.
5．(2014年高考全國卷1)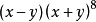
的展開式中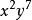
的係數是_________ .
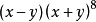
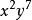
解析：原式可化為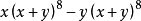
，依題兩部分的
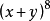中x分別要取1個和取2個，故 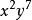的係數是
=-20.
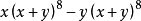
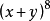
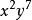
6．(2010年高考遼寧卷)
的展開式中的常數項為_________.
解析：原式可化為
，依題三部分中
的x分別要取3個、不能取任何值、取2個，故常數項是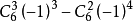
=-5.
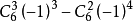
7．(2008年高考浙江卷) 在(x-1)(x-2)(x-3)(x-4)(x-5)的展開式中，含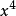
的項的係數是( )
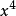
A．-15 B．85 C．-120 D．274
解析：依題5個括弧內x要取4個剩下一個取常數，故x的項的係數是-1-2-3-4-5=-15，故選A.
8．(2008年高考四川卷)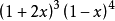 
展開式中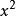
的係數為________.
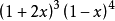
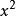
解析：依題可分三類：2x不取-x取2個，2x取1個-x取1個，2x取2個-x不取，故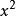 的係數是
=-6.
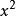
9．求 的展開式中x的係數.
解法一(化成兩個二項式的積)：因為 =[(x+4)(x-1)]=(x+4)(x-1)，依題可分二類：(x+4)與(x-1)中的x分別取1個、不取，和x分別不取，取1個，所以x的係數是 =-768．
解法二(直接套用組合推導法)： 看成4個
相乘，依題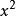 不取，3x取1個，剩下的-4取3個，所以x的係數是
=-768.
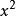
10． 已知
的第五項的二項式係數與第三項的二項式係數之比是14:3，求展開式中的常數項與二項式係數的最大值。
解：依題
=14:3， 得(n-2)(n-3)=56， 解得n=10或n=-5(捨去).
從而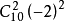
中的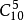
取2個，得到常數項為
=180；
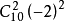
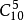
二項式係數的最大值為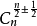
=252.
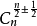
說明：二項展開式相應的二項式係數具有對稱性，先增後減，中間項的二項式係數最大。若n是偶數，最大的二項式係數是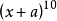
；若n是奇數，中間項有兩項，最大的二項式係數是
。
二、已知二項展開式的某項或某項的係數，求相應的常數.
11．(2014年高考全國卷2)
的展開式中的
係數為15，則a=______.
解析：依題a要取3個，故係數是
=15，解得a=
.
12．(2014年高考湖北卷) 若二項式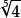
的展開式中的
係數是84，則實數a= ( )
A．2 B．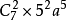
C．1 D．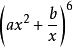
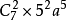
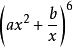
解析：依題2x要取2個，故係數是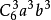
=84，解得a=1，故選C.
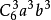
13．(2014年高考山東卷) 若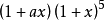
的展開式中x的項係數為20，則a+b的最小值為______.
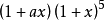
解析：依題ax要取3個，故係數是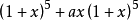
=20，解得ab=1，
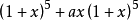
由a+b≥2ab=2，得所求最小值為2.
14．(2013年高考新課標全國卷2) 已知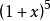
的展開式中x的係數為5，則a=( )
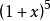
A．－4 B．－3 C．－2 D．－1
解析：原式可化為
，依題兩部分的中x分別要取2個和取1個，故x的係數為=5，解得a=－1，故選D.
