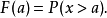累積分布函式

累積分布函式(Cumulative Distribution Function)，又叫分布函式，是機率密度函式的積分，能完整描述一個實隨機變數X的機率分布。一般以大寫CDF標記,，與機率密度函式probability density function（小寫pdf）相對。

基本介紹

• 中文名：累積分布函式
• 外文名：cumulative distribution function
• 定義：F(a)=P(x<=a)
• 歸類：數學函式
• 縮寫：CDF

定義

對於所有實數 ，累積分布函式定義如下：

即累積分布函式表示：對離散變數而言，所有小於等於a的值出現機率的和。

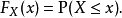
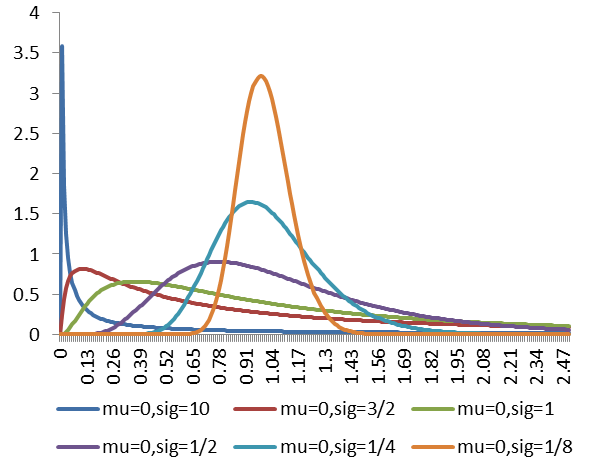
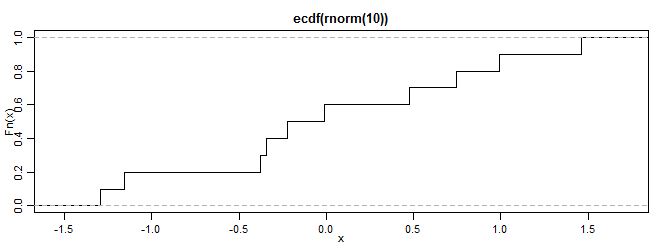圖1.累積分布函式

性質

1.有界性

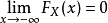
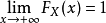
2.單調性

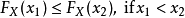
3.右連續性

之值落在一區間(a,b]之內的機率為

一隨機變數X的CDF與其pdf的關係為

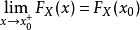
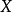
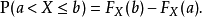
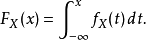
反函式

若累積分布函式F是連續的嚴格增函式，則存在其反函式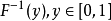。累積分布函式的反函式可以用來生成服從該隨機分布的隨機變數。

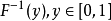
設若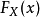是機率分布X的累積分布函式，並存在反函式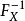。若a是[0,1)區間上均勻分布的隨機變數，則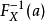服從X分布。

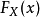
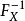
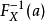
互補累積分布函式

互補累積分布函式（complementary cumulative distribution function、CCDF），是對連續函式，所有大於a的值，其出現機率的和。