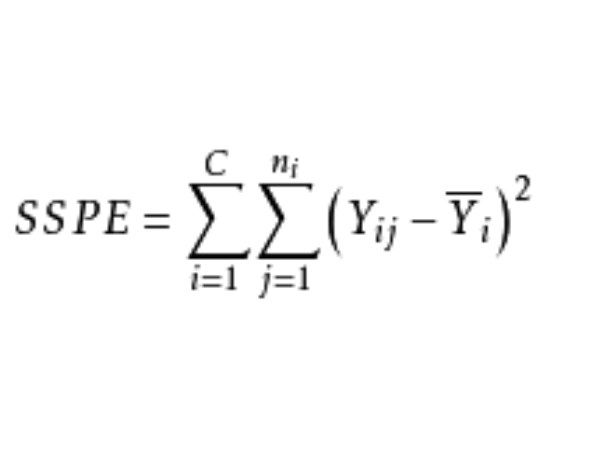純誤差平方

殘差是由兩部分組成的，一部分是隨機的，即使模型擬合得再好，它也消除不了，稱為隨機誤差或純誤差；另一部分與模型有關，模型合適，這部分的值就小，模型不合適，這部分的值就大，稱為失擬誤差，對應的殘差平方和由兩部分構成，一部分是純誤差平方和，另一部分是擬合不佳所引起的擬合誤差平方和。純誤差平方和(pure error sum of squares;SSPE或SS_PE等)是模型失擬的檢驗中所使用的量，其自由度為∑ (n_i-1)=n-c，將純誤差平方和除以自由度即為純均方誤差，通常用MSPE表示。

基本介紹

• 中文名：純誤差平方和
• 外文名：pure error sum of squares
• 所屬學科：數學（數理科學）
• 符號表示：SSPE，SSP等
• 套用：失擬檢驗等
• 相關概念：殘差平方和，擬合誤差平方和等

基本介紹

在重複試驗的回歸模型中，設自變數的取值水平共C個，共試驗n次，其中每個水平F重複獨立試驗n_i次(∑n_i=n)。設因變數在第i水平下的第j次觀察值為Y_ij，i=1，…，C，j=1，…，n_i，令

表示第i水平下因變數的平均數，則

稱為純誤差平方和，其自由度為，SSPE是模型失擬的檢驗中所使用的量。將誤差平方和除以自由度即為純均方誤差，通常用MSPE表示，即

相關知識

失擬檢驗是一種用來判斷回歸模型是否可以接受的檢驗。判斷模型好壞主要通過殘差分析，而殘差是由兩部分組成的；一部分是隨機的，即使模型擬合得再好，它也消除不了，稱為隨機誤差或純誤差；另一部分與模型有關，模型合適，這部分的值就小，模型不合適，這部分的值就大，稱為失擬誤差。失擬檢驗就是以失擬誤差對純誤差的相對大小來作判斷的： 倘失擬誤差顯著地大於純誤差，那么就放棄模型；如並不顯著地大於純誤差，那么就可以接受該模型。失擬檢驗的前提是要求在自變數x的若干值處進行重複試驗，設在x_j處有n_j次重複試驗 (j=1，2，…，c)，記

則有

其中： SSE—殘差平方和，SSPE—純誤差平方和，SSLF—失擬的平方和（擬合誤差平方和）。SSE，SSPE，SSLF的自由度分別為n-p-1，n-c，c-p-1。在獨立、正態及等方差假定之下

對於給定置信度水平 (1-α)，如果F<F_α(c-p-1，n-c)就認為失擬是不顯著的，就接受該模型；如果F>F_α(c-p-1，n-c)，則認為失擬不顯著，因而模型可以拒絕。儘管失擬檢驗原則上能夠檢驗任何種類的回歸模型，但通常用它來檢驗模型的線性假設是否合理。

定理

設有m個試驗點，在每一個處有次重複，其試驗結果為，令 ，則MS_P是 的一個無偏估計。當 相互獨立時， 。且 的分布不依賴於 的選擇。

證明 從略。

令表示模型在點外的擬合值()，則在點外的殘差為

從而有

即

其中SS_E為殘差平方和，SS_P為純誤差平方和，SS_L為擬合誤差平方和。並且對應於(1)有如下的自由度分解：

其中p為模型未知參數的個數。顯然，m≥p。如果m=p，則模型無擬合誤差，即數據完全擬合模型。從(1)可知，模型的殘差平方和由兩部分構成。一部分是純誤差平方和，另一部分是擬合不佳所引起的誤差平方和。

令，則，這裡。由此，可以用於檢驗模型擬合的好壞。