在數學的紐結理論中，扭結多項式指的是一類以多項式表達的紐結不變數（knot invariant），而此類多項式的係數則表示它所代表的紐結的一些性質。
基本介紹
- 中文名：紐結多項式
- 外文名：knot invariant
- 分類：數理科學
歷史,多項式,參見,特定的紐結多項式,相關主題,
歷史
第一個已知的紐結多項式，也就是所謂的亞歷山大多項式（Alexander polynomial），是由詹姆斯·韋德爾·亞歷山大在1923年引進的，但其他的紐結多項式卻一直都沒找到，直到近六十年後。
在1960年代，約翰·何頓·康威找出了一個對於亞歷山大多項式的某版本的糾結關係（skein relation），這又被稱為所謂的康威─亞歷山大多項式（Alexander–Conway polynomial）。糾結關係的重要性直到1980年代前期沃恩‧锺斯（Vaughan Jones）發現锺斯多項式（Jones polynomial）前都未被理解。這導致了更多紐結多項式的發現，如所謂的HOMFLY多項式。
锺斯發現該多項式不久後，路易‧考夫曼（Louis Kauffman）便注意到說锺斯多項式可藉由狀態和模型（state-sum model）來計算，這牽涉到所謂的括弧多項式（Bracket polynomial），該多項式為框多項式（framed knot）的一個不變數。這開啟了連結紐結理論和統計力學間關係的研究。
在1980年代晚期，這方面有兩個重要的突破。愛德華‧衛頓（Edward Witten）指出了锺斯多項式及相似的锺斯式不變數，有個以陳─西蒙斯理論（Chern–Simons theory）進行解釋的方法。維克托‧瓦西里耶夫（Viktor Vassiliev）和米哈伊爾‧高薩羅夫（Mikhail Goussarov）則開始了紐結的有限類不變數（finite type invariant）的理論。
近年來，亞歷山大多項式已被證明與弗洛爾同調（Floer homology）相關。
多項式
多項式（Polynomial）是代數學中的基礎概念，是由稱為未知數的變數和稱為係數的常數通過有限次加減法、乘法以及自然數冪次的乘方運算得到的代數表達式。多項式是整式的一種。未知數只有一個的多項式稱為一元多項式；例如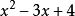
就是一個一元多項式。未知數不止一個的多項式稱為多元多項式，例如
就是一個三元多項式。
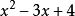
可以寫成只由一項構成的多項式也稱為單項式。如果一項中不含未知數，則稱之為常數項。
多項式在數學的很多分支中乃至許多自然科學以及工程學中都有重要作用。
參見
特定的紐結多項式
- 亞歷山大多項式（Alexander polynomial）
- 括弧多項式（Bracket polynomial）
- HOMFLY多項式
- 锺斯多項式（Jones polynomial）
- 考夫曼多項式（Kauffman polynomial）
相關主題
- 糾結關係（skein relation）
