納什均衡是博弈論中一種解的概念，它是指滿足下面性質的策略組合：任何一位玩家在此策略組合下單方面改變自己的策略（其他玩家策略不變）都不會提高自身的收益。
基本介紹
- 中文名：納什均衡
- 外文名：Nash equilibrium
- 別名：非合作博弈均衡
- 解釋：策略組合
簡介,歷史背景,分類,經典案例,囚徒困境,硬幣正反,重要影響,
簡介
納什均衡（Nash equilibrium），又稱為非合作博弈均衡，是博弈論的一個重要術語，以約翰·納什命名。在一個博弈過程中，無論對方的策略選擇如何，當事人一方都會選擇某個確定的策略，則該策略被稱作支配性策略。如果任意一位參與者在其他所有參與者的策略確定的情況下，其選擇的策略是最優的，那么這個組合就被定義為納什均衡。
一個策略組合被稱為納什均衡，當每個博弈者的均衡策略都是為了達到自己期望收益的最大值，與此同時，其他所有博弈者也遵循這樣的策略。
歷史背景
關於納什均衡的普遍意義和存在性定理的證明等奠定非合作博弈理論發展基礎的重要成果，是約翰·納什在普林斯頓大學攻讀博士學位時完成的。實際上，博弈論的研究起始於1944年約翰·馮·諾依曼（Von Neumann）和奧斯卡·摩根斯特恩（Oscar Morgenstern）合著的《博弈論和經濟行為》。然而卻是納什首先用嚴密的數學語言和簡明的文字準確地定義了納什均衡這個概念，並在包含“混合策略（mixed strategies）”的情況下，證明了納什均衡在n人有限博弈中的普遍存在性，從而開創了與諾依曼和摩根斯坦框架路線均完全不同的“非合作博弈（Non-cooperative Game）”理論，進而對“合作博弈（Cooperative Game）”和“非合作博弈”做了明確的區分和定義。阿爾伯特·塔克（Albert tucker）教授評價其論文，“這是對博弈理論的高度原創性和重要的貢獻。它發展了本身很有意義的n人有限非合作博弈的概念和性質。並且它很可能開拓出許多在兩人零和問題以外的，至今尚未涉及的問題。在概念和方法兩方面，該論文都是作者的獨立創造。”
分類
納什均衡可以分成兩類：“純策略納什均衡”和“混合策略納什均衡”。
要說明純策略納什均衡和混合策略納什均衡，要先說明純策略和混合策略。
所謂純策略是提供給玩家要如何進行博弈的一個完整的定義。特別地是，純策略決定在任何一種情況下要做的移動。策略集合是由玩家能夠施行的純策略所組成的集合。而混合策略是對每個純策略分配一個機率而形成的策略。混合策略允許玩家隨機選擇一個純策略。混合策略博弈均衡中要用機率計算，因為每一種策略都是隨機的，達到某一機率時，可以實現收益最優。因為機率是連續的，所以即使策略集合是有限的，也會有無限多個混合策略。
當然，嚴格來說，每個純策略都是一個“退化”的混合策略，某一特定純策略的機率為1，其他的則為0。
故“純策略納什均衡”，即參與之中的所有玩家都使用純策略；而相應的“混合策略納什均衡”，之中至少有一位玩家使用混合策略。並不是每個博弈都會有純策略納什均衡，例如“錢幣問題"就只有混合策略納什均衡，而沒有純策略納什均衡。不過，還是有許多博弈有純策略納什均衡（如協調博弈，囚徒困境和獵鹿博弈）。甚至，有些博弈能同時有純策略和混合策略均衡。
經典案例
囚徒困境
假設有兩個小偷A和B聯合犯事、私入民宅被警察抓住。警方將兩人分別置於不同的兩個房間內進行審訊，對每一個犯罪嫌疑人，警方給出的政策是：如果一個犯罪嫌疑人坦白了罪行，交出了贓物，於是證據確鑿，兩人都被判有罪。如果另一個犯罪嫌疑人也作了坦白，則兩人各被判刑8年；如果另一個犯罪嫌疑人沒有坦白而是抵賴，則以妨礙公務罪（因已有證據表明其有罪）再加刑2年，而坦白者有功被減刑8年，立即釋放。如果兩人都抵賴，則警方因證據不足不能判兩人的偷竊罪，但可以私入民宅的罪名將兩人各判入獄1年。
A╲B | 坦白 | 抵賴 |
坦白 | -8，-8 | 0，-10 |
抵賴 | -10，0 | -1，-1 |
關於案例，顯然最好的策略是雙方都抵賴，結果是大家都只被判1年。但是由於兩人處於隔離的情況，首先應該是從心理學的角度來看，當事雙方都會懷疑對方會出賣自己以求自保、其次才是亞當·斯密的理論，假設每個人都是“理性的經濟人”，都會從利己的目的出發進行選擇。這兩個人都會有這樣一個盤算過程：假如他坦白，如果我抵賴，得坐10年監獄，如果我坦白最多才8年；假如他要是抵賴，如果我也抵賴，我就會被判一年，如果我坦白就可以被釋放，而他會坐10年牢。綜合以上幾種情況考慮，不管他坦白與否，對我而言都是坦白了划算。兩個人都會動這樣的腦筋，最終，兩個人都選擇了坦白，結果都被判8年刑期。
基於經濟學中“理性的經濟人”的前提假設，兩個囚犯符合自己利益的選擇是坦白招供，原本對雙方都有利的策略不招供從而均被判處一年就不會出現。這樣兩人都選擇坦白的策略以及因此被判8年的結局，納什均衡”首先對亞當·斯密的“看不見的手”的原理提出挑戰：按照斯密的理論，在市場經濟中，每一個人都從利己的目的出發，而最終全社會達到利他的效果。但是我們可以從“納什均衡”中引出“看不見的手”原理的一個悖論：從利己目的出發，結果損人不利己，既不利己也不利他。
硬幣正反
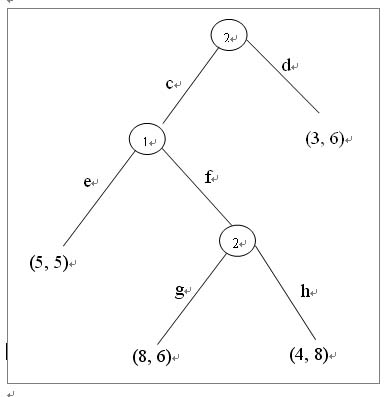
你正在圖書館枯坐，一位陌生美女主動過來和你搭訕，並要求和你一起玩個數學遊戲。美女提議：“讓我們各自亮出硬幣的一面，或正或反。如果我們都是正面，那么我給你3元，如果我們都是反面，我給你1元，剩下的情況你給我2元就可以了。”那么該不該和這位姑娘玩這個遊戲呢？這基本是廢話，當然該。問題是，這個遊戲公平嗎？
每一種遊戲依具其規則的不同會存在兩種納什均衡，一種是純策略納什均衡，也就是說玩家都能夠採取固定的策略(比如一直出正面或者一直出反面)，使得每人都賺得最多或虧得最少；或者是混合策略納什均衡，而在這個遊戲中，便應該採用混合策略納什均衡。
你\美女 | 美女出正面 | 美女出反面 |
你出正面 | +3，-3 | -2，+2 |
你出反面 | -2，+2 | +1，-1 |
假設我們出正面的機率是x，反面的機率是1-x，美女出正面的機率是y，反面的機率是1-y。為了使利益最大化，應該在對手出什麼的時候我們的收益都相等（不然在這個遊戲中，對方可以改變正反面出現的機率讓我們的期望收入減少），由此列出方程就是
納什均衡
解方程得y=3/8。
同樣，美女的收益，列方程
解得x也等於3/8，而美女每次的期望收益則是
元。這告訴我們，在雙方都採取最優策略的情況下，平均每次美女贏1/8元。
其實只要美女採取了(3/8,5/8)這個方案，不論你再採用什麼方案，都是不能改變局面的。
重要影響
納什均衡理論奠定了現代主流博弈理論和經濟理論的根本基礎，正如克瑞普斯（Kreps，1990）在《博弈論和經濟建模》一書的引言中所說，“在過去的一二十年內，經濟學在方法論以及語言、概念等方面，經歷了一場溫和的革命，非合作博弈理論已經成為範式的中心……在經濟學或者與經濟學原理相關的金融、會計、行銷和政治科學等學科中，現在人們已經很難找到不懂納什均衡能夠‘消費’近期文獻的領域。”納什均衡的重要影響可以概括為以下六個方面
1．改變了經濟學的體系和結構。非合作博弈論的概念、內容、模型和分析工具等，均已滲透到個體經濟學、總量經濟學、勞動經濟學、國際經濟學、環境經濟學等經濟學科的絕大部分學科領域，改變了這些學科領域的內容和結構，成為這些學科領域的基本研究範式和理論分析工具，從而改變了原有經濟學理論體系中各分支學科的內涵。
2．擴展了經濟學研究經濟問題的範圍。原有經濟學缺乏將不確定性因素、變動環境因素以及經濟個體之間的互動作用模式化的有效辦法，因而不能進行微觀層次經濟問題的解剖分析。納什均衡及相關模型分析方法，包括擴展型博弈法、逆推歸納法、子博弈完美納什均衡等概念方法，為經濟學家們提供了深入的分析工具。
3．加強了經濟學研究的深度。納什均衡理論不迴避經濟個體之間直接的互動作用，不滿足於對經濟個體之間複雜經濟關係的簡單化處理，分析問題時不只停留在巨觀層面上而是深入分析表象背後深層次的原因和規律，強調從微觀個體行為規律的角度發現問題的根源，因而可以更深刻準確地理解和解釋經濟問題。
4．形成了基於經典博弈的研究範式體系。即可以將各種問題或經濟關係，按照經典博弈的類型或特徵進行分類，並根據相應的經典博弈的分析方法和模型進行研究，將一個領域所取得的經驗方便地移植到另一個領域。
5．擴大和加強了經濟學與其他社會科學、自然科學的聯繫。納什均衡之所以偉大，就因為它普通，而且普通到幾乎無處不在。納什均衡理論既適用於人類的行為規律，也適合於人類以外的其他生物的生存、運動和發展的規律。納什均衡和博弈論的橋樑作用，使經濟學與其他社會科學、自然科學的聯繫更加緊密，形成了經濟學與其他學科相互促進的良性循環。
6．改變了經濟學的語言和表達方法。在進化博弈論方面相當有造詣的日本經濟學家神取道宏（Kandori Michihiro，1997）對保羅·薩繆爾森（Paul Samuelson）的名言“你甚至可以使一隻鸚鵡變成一個訓練有素的經濟學家，因為它必須學習的只有兩個詞，那就是‘供給’和‘需求’”，曾做過一個幽默的引申，他說，“現在這隻鸚鵡需要再學兩個詞，那就是‘納什均衡’”。
