紅珠實驗

紅珠實驗(Red Bead Experiment) 是著名質量學家戴明設計的兩個實驗之一（另一個是漏斗實驗），此實驗說明了儘管生產程式是一樣的地嚴格，但是還是會無可避免的出現各種變異，即質量缺陷問題。

基本介紹

• 中文名：紅珠實驗
• 外文名：Red Bead Experiment
• 設計者：戴明
• 實驗問題：質量缺陷問題

儀器

①4000粒木珠，直徑約3毫米，其中800粒為紅色，3200粒為白色；

②一個有50個凹洞的勺子，每5個凹洞1排，共10排，凹洞大小與木珠相當，一次可盛起50粒木珠(代表工作量)；

③一個長方形容器，大小恰好能夠讓一把勺子在裡頭撈珠子。

目的

戴明要求學員們想想假如他們未曾看過這場實驗，會對結果做出什麼預測？假設共有4000顆珠子，其中3200（80%）是白珠，800顆（20%）是紅珠，則每天平均數，會不會落在某個特定的數字上，部分人大膽地推論：假如日產量是50顆，一段時間下來，紅珠的數字應該為平均日產量的20%，也就是10顆。所以有人喊出了“10顆”。戴明說：“你們錯了。”戴明解釋道，你們為什麼說它會落在10呢，數據出現的是11.8、8.5、8.3、8.0的下滑趨勢。說10隻是一廂情願的想法。因為你們學習統計理論時，沒有學到它的精髓，不知道如何利用。因為我們看到的平均數不是10，而是好像還要低些。既然如此，一定有某些變數影響整個過程。

戴明要求大家換個角度思考。戴明說：“紅珠和白珠當然不同。你們知道紅珠是怎樣製造出來的嗎？你先把它們都製成白珠。鋪在桌上讓它們自然晾乾。將其中一部分浸在紅色顏料中，然後再鋪在桌上晾乾。這樣就有紅珠也有白珠。紅珠由於顏料而較重。但是，你們卻告訴我，會落在10，因為盒子裡有20%是紅珠。”戴明接著說：“勺子十分重要。我已經使用一號勺子30年了；我當年教日本工程師時就是用它。這支勺子每次平均可撈到11.3顆紅珠，這是實驗100次以上獲得的數值。二號勺子平均可撈得9.6顆。今天用的三號勺子，平均可撈到9.4顆或9.2顆。”最後戴明指出，假如我們所用的統計管制水準還算過得去，就會固定在“某個位置”。我們會建立起一套可信度。假如我們現在就應該計畫未來，的數值大約可以說是9.2，但不能確定到底離這有多遠。一定有相當大的彈性空間才行。

實驗的目的是要證實一個事實：經理人為員工所設下的標準，常常超出員工所能控制的範圍。通過這項實驗也可看出，如何用統計方法找出問題根源。

步驟

第一步 招聘作業員

每場研討會的學員在第二天下午一面忙著消化午餐，一面消化“新哲學”的同時，戴明博士總會進行一項他所稱的“笨實驗”；但他保證，這項實驗將令人永遠難忘。他一一拿了實驗器材。首先是一個裡頭裝著許多豌豆般大小紅白木珠的塑膠盒；其次，是一支上面有50個凹洞的把杓(每5個凹洞一排，共10排，凹洞大小與木珠相當)；然後是另一個塑膠盒；大小恰足以讓把杓在裡頭撈珠子。接下來的一小時裡，實驗在一片歡笑中開始了。儘管現場笑聲不斷，這場木珠實驗卻深刻。凸顯出一項事實：經理人為員工所設下的標準，往往超出他們所能控制的範圍。這項實驗同時也顯示出，如何用統計方法找出問題來源。會場前端成了生產線，戴明博士自己則扮演可怕的工頭。他嚴厲地宣布：“我們的工作是‘產出’白珠，因為顧客不收紅珠子。” 他從聽眾中招募人員，加入生產線，並開玩笑的說：“女士優先。”他的求才啟事如下：“本公司誠徵作業員六名，需要高度熱忱；檢驗員2名——因為本分司作業錯誤百出，冗員充斥；檢驗長一員——這是本公司唯一沒做錯的事——檢驗員獨立執行計算，不需尋求共識。另征記錄員1名，此乃重要職務……須具備書寫及加法能力。因為他要負責登記姓名，並記錄產量。"

第二步 作業員各就各位

有位男士走出來，到會場前端應徵記錄員。戴明博士裝出一副嚴厲的樣子質問：“你會寫字嗎?會寫數字嗎?加法也懂?好，請就位，我會把你放在薪水單上。”他以類似的方式，錄用了兩名檢驗員和一名檢驗長。(他問的問題之一是：你會數數嗎?你能從一數到一二十嗎?那好，去拿張紙吧。)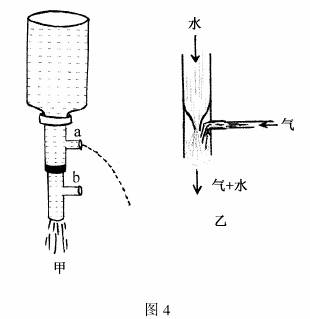

大氣壓實驗

接著他開始招募生產線作業員。“現在我們需要6名有工作熱忱的作業員，學歷不拘，但必須有工作熱忱。好，我現在看到有一個人舉手，請到前面來。1個，2個，3個，4個，5個，6個。好，都請到前面來。"

工作人員就位後，戴明博士開始講解任務。他模仿工頭的權威口吻說：“紀錄員請準備上工。你隨時可以開始登記檢驗員姓名。”接著對作業員說：“6名有工作熱忱的作業員聽著：你們不可以和檢驗員攀談。你們的位置就在這裡(身體往右挪)”又說：“記錄員要有筆，我借給你一支，不過要記得還回來。好，先寫下自己的名字。檢驗員、檢驗長、6名熱忱的作業員，請各就各位。” 戴明博士逐一查對員工身份後說：“你們當中哪個人的素質能力是全體成員的平均水準?”他注視著其中一名作業中狄克說：“你是平均水準的那位嗎?” 狄克回答：“應該是。” 戴明說：好!站這裡，那么另外5人都在水準之上(聽眾大笑)。就按這個順序排列。平均水準的那個人，叫狄克是吧?好，帕特、包伯、……不要太快，記錄員沒辦法寫太快。好，霍斯特、……等一下，全亂了，擦掉重寫。

“順序對我們來說非常重要。平均水準的人排第一，接下來是帕特、包伯。別急，別太快。再來是史帝夫、霍斯特、戴夫。”

名字依序記下來之後，戴明開始發號施令了：“你們要先經過3天的試用期，這段期間將會照樣給薪。我將扮演工頭。但既然這裡其他人都不了解我們的工作到底該做些什麼，我先親自出馬。我們的任務是‘產出’白珠子。”

第三步 紅珠白珠落滿盤

“這個地方是有規則的，在我說出之前，先告訴我，你們願不願意全力以赴?”作業員一致點頭。戴明接著說：“程式是這樣的，它們很明確，必須一步一步來，不可有任何改變。必須完全遵照程式，不準中途辭職。就算你們可能被炒魷魚，也不可主動提出。大家都聽清了嗎?” 戴明博士把兩個盒子中較大的那個拿出來；裡頭混裝著800顆紅珠、3200顆白珠。他右手抓著大盒子說：“我們總共有兩個容器，尺寸不同，一大一小。清楚嗎?拿盒子時你們要抓住兩個容器較寬的一邊，懂嗎?你們要把珠子從大容器倒到小容器，從最靠近的角落倒進去，距離保持‘5厘米’。他特彆強調‘5厘米’，引來一陣笑聲。他一邊倒珠子，一邊告訴聽眾：“我們的程式很嚴格。"他先把珠子倒到小容器，又倒回大容器，讓兩種珠子混合均勻。 “5厘米!再倒回來。”他提高聲調：“抓住兩個容器寬的那一邊，從最靠近的一角倒進去，這就是你們完成每日工作的方法。我們的一套工作程式是：每天取50 顆，不多也不少。任務是‘產出’白珠子——我們的標準是50顆，紅珠子白珠子都要算，但記住，顧客不接受紅珠。

實驗材料

“你們把珠子倒進大容器後，要拿起把杓，插入珠子堆里。把杓不要晃動，以免紅珠子掉了出來。假如紅珠子掉在地上，就得停止生產。” 他停頓一下說：“你們準備開始胼手胝足的幹活吧!” 戴明博士繼續示範。他把把杓插進大容器里，讓50個洞都裝了珠子。雖然實際操作要比表面看起來困難，不過每位“作業員們”最後都學會了。“把杓子往下推，推到底。拿出來，不要晃。”戴明博士在旁提醒。

他問：“你們自認為已經了解了嗎?”“作業員”一致肯定地點頭。

戴明博士開玩笑說：“我自己故意舀了些紅珠子，好讓你們知道它們長什麼樣子。” 他繼續解釋下一步：“帶你的成果到一號檢驗員那裡，他會大聲把他算的數念出來。接著到2號檢驗員那裡去，他會記下數字。檢驗長則比較這些數字。” 戴明告訴檢驗長：計算工作由你負責。假如發現數字有出入，其中必有一人是錯的。你要負責找出來，並大聲喊出正確數目。你認為工作交代得夠清楚了嗎?明白了嗎?知道你不能有所背離的嗎?我們的程式非常嚴格，正如我所描述的。假如你對算出來的數字滿意，就可以讓那位作業員離開。一定要對結果滿意，才可以放人。然後，他便可以把當天的成果倒回原來取出的容器去。清楚了嗎?現在，那位‘平均水準’的男士可以開始了。” 狄克抓起大容器，將珠子倒進小容器里，戴明博士大聲吼著：“5厘米!” 狄克把杓子挖進大容器內，努力舀取白珠子。戴明博士問其他作業員：“你們有沒有認真看?注意看他是怎么做的。如果他撈到紅珠子，看他是怎么撈到的。你們要避免重蹈覆轍。”

戴明轉頭向聽眾說明：“這就帶來恐懼了……”

第四步 紅珠掙扎戰

狄克裝滿杓子後，稍微傾斜了一下，讓多餘的珠子滾出來。戴明博士告訴他：“現在，到1號檢驗員那邊去，靜靜的把他計算的結果記在紙上。然後，到2號驗員那裡去。檢驗長將會確定數目，並宣布出來。” 檢驗長保羅遵照指示，大聲宣布紅珠子的數目：“14顆。” 戴明博士故作煩惱：“多達14顆，我要說我們真是出師不利”。(全場爆笑)他把全部“作業員”聚在一起，對他們說：“我得讓你們知道。我們的客戶只收白珠子。所以我們的職責是：製造白珠子，而不是紅珠子。14顆!”他語調哀淒。“這樣一來，我們怎么立足。” 接下來輪到第二位帕特小姐。戴明提醒她：“5厘米!慢慢來，不要晃。珠子會滾出來。把成果拿給1號檢驗員計算。” 聽眾聽到數目是“17”時，紛紛發出不滿的嘆息。工頭戴明看來更苦惱。他臉色陰沈沈的的對帕特說：“我要和你談談。我們要產出白珠子。你剛剛有沒有注意看?為什麼還是產出紅珠呢?我真不明白。下一位!” 這回，第3位作業員馬伯的成績略有進步，只有11顆紅珠。

紅珠實驗

戴明博士高興的大叫：“哈!這就是我所說的改善了。不過，改善得還不夠。”他轉向其他作業員：“你們都看到了是怎么做的了吧?好，我們現在開始努力改善。這就是我們所需要的……持續不斷的改善。” 下一位作業員史帝夫的成績更好，只有8顆紅珠。戴明博士滿意的說：“這才叫改善——持續的改善，好極了，這就是我們所需要的。改善之處愈來愈多。一次比一次好。” 但第5名作業員霍斯特的紅珠卻增為12顆。戴明博士責罵道：“這不叫改善!恐怕你弄錯了。”他把注意力移到最後一名作業員戴夫身上說：“好，戴夫，現在你必須表現優異，把平均水準拉回來。”

戴夫的成績是9顆紅珠，是全部人中次少的。但工頭戴明並不滿意，他對作業員說：“我要告訴你們。我們的程式十分嚴格，不準有差異。但現在成果很差。我不明白為什麼差異程度這么大：史帝夫八顆，帕特17顆。程式相同，進料相同，紅珠也都占20%。這么嚴格的程式，照理說不應有變異才對，為什麼卻從8顆到 17顆都有。不可思議，17是8的兩倍多呢。”他以無法置信的聲調重複：“不應該有變異才對。我們的程式固定，每個人都在相同的程式下工作，規則完全相同。身為工頭，我只能說對你們的表現表示失望。”

第五步 鼓勵與施壓

“現在，我們接下來繼續‘第二天’的工作，還是由‘平均水準’的那個人先開始。身為工頭，我希望你們能有所進步。” 狄克“第二天”撈到10顆紅珠，比前一天的14顆進步。戴明博士恭喜他說：“狄克，這就是我所說的進步。” 下個作業員帕特只撈到5顆紅珠，引來一陣歡呼，是目前最好的成績。戴明博士以帕特為例，激勵其它作業員：“假如帕特只撈到5顆，誰都可以只撈到5顆。超過 5顆的教人無法理解。我們的程式嚴格，它們完全相同……只是周而復始。不該變生變異才對。”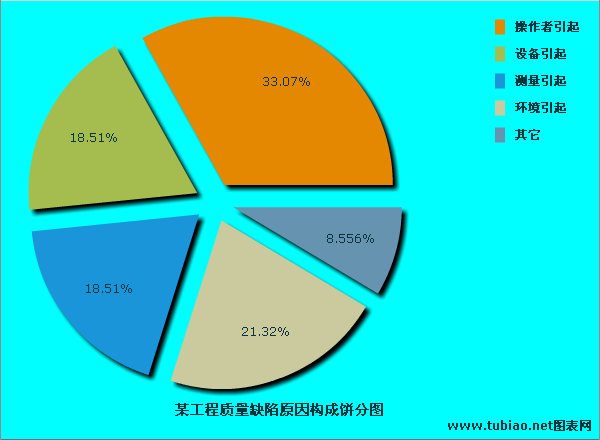

質量缺陷

巴伯6顆紅珠的優異成績，也受到稱讚。接下來霍斯特11顆，得到“合格”的評語：“比昨天進步，即使只有一點點，但也不錯了。”他對最後一位戴夫說：“你現在得彌補同伴的不良表現了。”當戴夫撈到11顆時，工頭戴明斥罵：“知道嗎，戴夫，你要為今天整體的成果欠佳負一部分責任。”他轉向所有作業員說：“我們所需要的是更好的成績。高層主管一直盯著這些數字。他們對我們的低產出非常不滿。而你們的工頭也無法理解為什麼變異那么大，我不明白。繼續加油吧。切記，你們的工作全靠你們的表現……不是保有工作，就是流落街頭。全看你們了。我們可以讓工廠繼續開著大門，否則上級就要把工廠給關了。”

“第三天”帕特撈到八顆紅珠的時候，工頭有點失望。他說：“帕特，我不明白。昨天你只撈到5顆，今天卻是8顆。這樣的差異令人無法理解。沒道理啊。記住——你的職位可能不保。” “第三天”將盡時，戴明把全部作業員召集在一起時，對他們說：“大家聽著，上頭一直在盯著這些數字，他們無法理解成績為何如此低落。他們已經決定，除非 ‘第四天’能有顯著的改善，否則就要關廠了。你們的工作能否保住，全看你們的表現。工廠已經入不敷出，一切就全靠你們了。要大大的改善才能繼續。現在，我希望你們盡情工作。這也許是你們的最後一天了。” 　 　作業員繼續“第四天”的工作。當最後一名作業員戴夫撈到10顆紅珠時，戴明博士大嘆：“要在這裡看到改善，真是太難了!我不了解為什麼做不到零缺點。”其他人的數目，分別是5、9、6、10顆紅珠。　戴明博士說：“上級一直注視著這些數字，他們非常不滿意我們的生產能力的低落，已經決定關廠了。走出大門前，請各位順道去領工資。謝謝大家。非常感謝。

質量管理

實驗做到現在，學員們開始了解到，用一模一樣的工具、完成一模一樣的任務、才智也一模一樣，生產的結果仍會時時變化。所以，管理者不該針對員工無法自己掌控的結果而責備他們。

接下來，戴明說明如何運用一個簡單的統計公式得出變異上下限。首先，他將所生產的紅珠總數220，除以撈取珠子的總次數(6個操作員做4天工作所撈取的總數)。結果我們得出每人每日平均數是9.2。這個日平均數被稱為 x=220/(6×4)=9.2

其次，他計算每人每天撈到紅珠的平均比例 ——就是撈到的全部珠子裡，紅珠所占的比例： =220/(6×4×50)=0.18

根據這些，再用公式算出“管制上限”(UCL, upper control limit)和“管制下限”(LCL, lower control limit): UCL=x 3 或 UCL=9.4 3

戴明認為，沒有人超過上限。6個人共試了24次，每次都在管理範圍之內。 戴明指出：如果在這套“生產線”的作業系統中，禁止改變，紅珠的數字將會在管制上限與下限之間波動，但不會超出界限。

戴明要求學員們想想假如他們未曾看過這場實驗，會對結果做出什麼預測？假設共有4000顆珠子，其中3200(80%)是白珠，800顆(20%)是紅珠，則每天平均數 ，會不會落在某個特定的數字上，部分人大膽地推論：假如日產量是50顆，一段時間下來，紅珠的數字應該為平均日產量的20%，也就是10顆。所以有人喊出了“10顆”。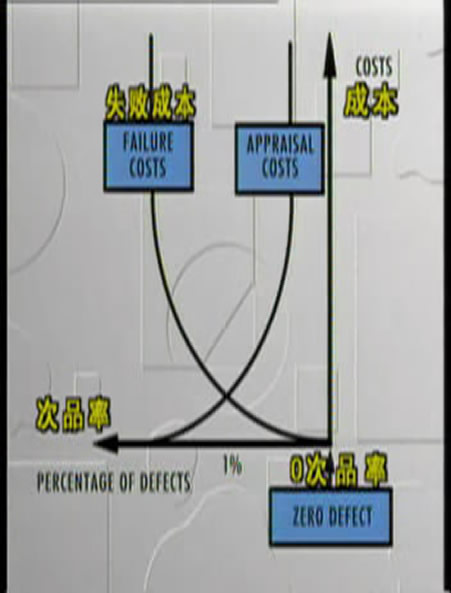

質量管理

戴明說：“你們錯了。”戴明解釋道，你們為什麼說它會落在10呢，數據出現的是11.8、8.5、8.3、8.0的下滑趨勢。說10隻是一廂情願的想法。因為你們學習統計理論時，沒有學到它的精髓，不知道如何利用。因為我們看到的平均數不是10，而是好像還要低些。既然如此，一定有某些變數影響整個過程。

戴明要求大家換個角度思考。戴明說：“紅珠和白珠當然不同。你們知道紅珠是怎樣製造出來的嗎？你先把它們都製成白珠。鋪在桌上讓它們自然晾乾。將其中一部分浸在紅色顏料中，然後再鋪在桌上晾乾。這樣就有紅珠也有白珠。紅珠由於顏料而較重。但是，你們卻告訴我， 會落在10，因為盒子裡有20%是紅珠。”戴明接著說：“勺子十分重要。我已經使用一號勺子30年了；我當年教日本工程師時就是用它。這支勺子每次平均可撈到11.3顆紅珠，這是實驗100次以上獲得的數值。二號勺子平均可撈得9.6顆。今天用的三號勺子，平均可撈到9.4顆或9.2顆。”

最後戴明指出，假如我們所用的統計管制水準還算過得去， 就會固定在“某個位置”。我們會建立起一套可信度。假如我們現在就應該計畫未來， 的數值大約可以說是9.2，但不能確定到底離這有多遠。一定有相當大的彈性空間才行。

戴明實驗

戴明在實驗中扮演主管，另外需要操作員6名、檢驗員2名、檢驗負責人1名、記錄員1名。操作員的工作是在紅白珠相混的容器中用勺子“產出”白珠，因為顧客只接收白珠；檢驗員要能區分紅珠和白珠，計數至20即可。在某次實驗中，戴明一共選了6名操作員：帕特、包伯、狄克、史蒂夫、霍斯特、戴夫。工作程式是每天取50顆，紅珠白珠都算，但記入工作量的只有白珠。狄克第一個先來。他把勺子挖進大容器內，盡力地舀取白珠。與此同時，戴明要求檢驗員記住他是怎么做的，以免後來的人重蹈覆轍。狄克舀完後，送到檢驗員處，檢驗員保羅宣布紅珠的數字是14顆。按照這個程式，後來的5位操作員帕特、包伯、史蒂夫、霍斯特、戴夫的紅珠數量依次是：17、11、8、12、9顆。在此過程中，戴明一直強調持續的改善，並且認為相同嚴格的程式，不應該存在變異才對。身為主管的戴明，對操作員們的表現表示失望。

紅珠實驗

第二輪實驗開始了。這一次狄克撈到10顆紅珠，比前一天的14顆有所進步。帕特只撈到5顆紅珠，這個好成績引來一陣歡呼。戴明以帕特為例，激勵其他操作員“假如帕特只撈到5顆，誰都能夠只撈到5顆。超過5顆的教人無法理解。我們的程式嚴格，只是周而復始，不應該發生變異才對。”巴伯6顆紅珠，霍斯特11顆紅珠，戴夫卻不如第一輪，11顆紅珠。身為主管的戴明斥罵了戴夫，並且認定他要負一部分責任。

第三輪實驗開始了。當看到帕特的成績是8顆紅珠時，戴明表現得非常失望。在第四輪的實驗中，最後一名操作員戴夫撈到了10顆紅珠，戴明大嘆：“要在這裡看到改善，真是太難了！我不了解為什麼做不到零缺點。”其他人的數字，分別是5、9、6、8、10顆紅珠。

始終記錄每位操作員紅珠數字的記錄員，在第四輪實驗結尾加總算出了數字，並計算每人平均日產量，以及全體的平均日產量，見如下統計圖表。

實驗做到現在，學員們開始了解到，用一模一樣的工具、完成一模一樣的任務、才智也一模一樣，生產的結果仍會時時變化。所以，管理者不該針對員工無法自己掌控的結果而責備他們。接下來，戴明說明如何運用一個簡單的統計公式得出變異上下限。首先，他將所生產的紅珠總數220，除以撈取珠子的總次數（6個操作員做4天工作所撈取的總數）。結果我們得出每人每日平均數是9.2。這個日平均數被稱為x=220/（6×4）=9.2其次，他計算每人每天撈到紅珠的平均比例——就是撈到的全部珠子裡，紅珠所占的比例：=220/（6×4×50）=0.18根據這些，再用公式算出“管制上限”（UCL，uppercontrollimit）和“管制下限”（LCL，lowercontrollimit）：UCL=x3或UCL=9.43戴明認為，沒有人超過上限。6個人共試了24次，每次都在管理範圍之內。戴明指出：如果在這套“生產線”的作業系統中，禁止改變，紅珠的數字將會在管制上限與下限之間波動，但不會超出界限。

結論

通過這個實驗可以得出如下結論：

(1)實驗本身是一個穩定的系統。在系統維持不變的情況下，工廠的產出水平及其變異是可預測的；事實上成本也是可預測的。

(2)所有的變異，包含工人之間產出紅珠數量的差異，以及每位工人每日產出紅珠數量的變異，均完全來自過程本身。沒有任何證據顯示哪一位工人比其他工人更高明。

(3)工人的產出顯示為統計管制狀態，也就是穩定狀態。工人們已經全力以赴，在現有狀況之下，不可能有更好的表現。

(4)在考績制度或員工評價中，將人員、團隊、銷售人員、工廠、部門排優劣順序是一種錯誤的做法，特別是它對員工的鬥志是一種打擊。因為員工的表現完全與努力與否無關。

(5)簡單以績效決定報酬是完全沒有意義的。工人的績效如此低落，以至失去工作，完全是被工作過程所左右。

(6)工頭給工人加薪或處罰，當作是對他們的表現進行獎勵與懲罰。實際上它獎勵與懲罰的是生產系統的表現，而不是工人的表現。

(7)這個實驗展示了拙劣的管理。由於程式僵化，工人根本沒有機會提供改善的建議。

(8)每個人在工作上都有責任去嘗試改進系統以提升自己和他人的績效。在工頭的規定之下，他們無從改進績效。

(9)管理者在沒有任何依據的情況下，事先已經固定了白珠的價格。

(10)檢驗員彼此獨立，這種做法是非常正確的。

(11)如果管理者能與珠子的供應商協商，降低進料中紅珠的比率，那是一個好訊息。

(12)即使事先已經知道紅珠在進料中所占比率(20%)，也無助於預測產出中紅珠占多大比例。

(13)管理者認定，過去表現最佳的三位工人，在將來也會有最佳的表現，這項假設並沒有任何理論依據。

(14)領班是系統的產物。換句話說，他的思維方式應該符合管理者的哲學。管理者交給他的職責是生產出顧客需求的產品，而他的報酬依賴工人的產出。