基本介紹
- 中文名：粘滯阻力
- 外文名：viscosity resistance
- 別 名：內摩檫力
- 貢獻科學家：牛頓、斯托克斯
- 粘滯係數：動力粘度、運動粘度
- 微觀表現：分子間引力、分子熱運動
簡述,流體粘性,試驗探究,粘滯係數,影響粘度因素,壓強,溫度,
簡述
粘滯阻力（viscosity resistance）
物體在粘滯性流體中運動時，由於緊靠物體表面的流體附於物體的表面而被帶走，於是在物體表面附近形成速度梯度，因而流層之間有內摩擦力，物體受到內擦阻力。這種由於流體的粘滯性直接產生的阻力叫做粘滯阻力。當物體運動速度不大，且物體的形狀是適宜的流線型時，物體的後邊沒有渦旋發生。在此情形下，物體所受的阻力就是粘滯阻力。
通過實驗總結，得出如下的規律:若物體相對於流體的運動速度很小時，其所受阻力F與物體相對於流體的運動速度v、流體的粘滯係數η及物體的線度l成正比。這一規律稱為斯托克定律。其比例係數隨物體的形狀而定，對於球形物體來說，其線度以半徑r表示。其比例係數為6π，即球形物體在粘滯性流體中運動時，所受到的粘滯阻力位：F=6πηrv，該式稱為斯托克定律。
流體粘性
流體都是具有粘性的。流體在管道中流動，需要在管道兩端建立壓強差或位置高度差；輪船在河流中行駛、飛機在空中飛行都需要動力的提供，這都是為了克服由於流體粘性所產生的阻力。
流體流動時產生內摩擦力的性質稱為流體的粘性，粘性是流體的固有物理屬性，但粘性只有在運動狀態下才能顯示出來。
在理論力學中所說的“與物體速度一次方成正比的阻力”，指的就是粘滯阻力。在空氣中運動速度不十分快的物體，受到的阻力主要是粘滯阻力。
形成流體粘性的原因有兩個方面：一是流體分子間的引力，當流體微團發生相對運動時，必須克服相鄰分子間的引力，這種作用類似物體間的相互摩擦，從而表現出摩擦力；二是流體分子的熱運動，當流體層之間作相對運動時，由於分子的熱運動，使流體層之間產生質量交換，由於流層之間的速度差別，必然產生動量交換，從而產生力的作用，使得相鄰的流體層之間產生摩擦力。不論氣體和液體，都存在分子之間的引力和熱運動，只是所占比重不同而已。對於氣體，由於分子距比較大，分子間的引力相對較小，而分子的熱運動卻非常強烈，因此構成氣體粘性的主要原因是分子的熱運動；對於液體，分子距非常小，分子之間的相互約束力非常大，分子的熱運動非常微弱，所以構成液體的粘性主要原因是分子間的引力。
試驗探究
牛頓在1687年用在流體中拖動的平板，做了著名的粘性流動實驗。如圖1所示，兩塊相隔一定距離的平行平板水平放置，其間充滿液體，下板固定不動，上板在F′力的作用下以
的速度沿x方向運動。實驗表明，粘附於上平板的流體在平板切向方向上產生的粘性摩擦力F即F′的反作用力，和兩平板間的距離h成反比，和平板的面積A、平板的運動速度v成正比，比例關係式如下：
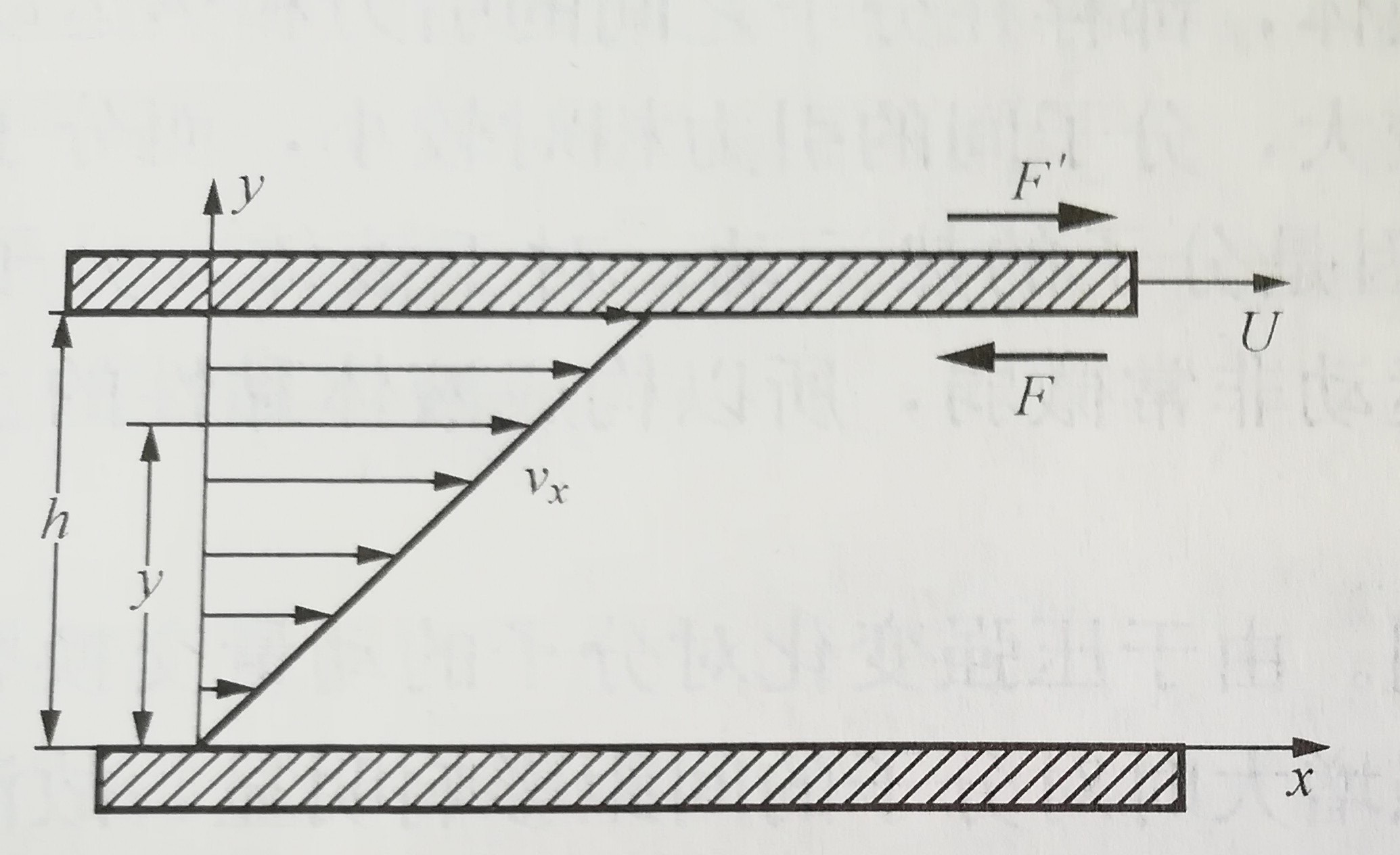圖1 粘滯阻力示意圖
圖1 粘滯阻力示意圖
式（1）中，μ為流體動力粘度，
表示在速度的垂直方向上單位長度上的速度增量，稱為速度梯度。如圖2所示，x方向上的速度用vx表示時，速度梯度可表示為
，此時速度梯度為一變數，在每一速度層上有不同的數值，將代入式（1），兩端同除以板的面積A，則可以得到作用在平板單位面積上的切應力
。
圖2 速度梯度圖
圖2 速度梯度圖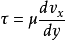
式（2）即為牛頓內摩擦定律，僅使用於層流流動的情況。
在流體緩慢流過靜止的物體或者物體在流體中運動時，流體內各部分流動的速度不同，存在粘滯阻力。粘滯阻力的大小與物體的運動速度成正比，即f∝v，可以寫為f = C1v，C1稱為粘滯阻力係數。斯托克斯測出球形物體在流體中緩慢運動時，所受到的粘滯阻力大小為：
f= 6πηvr （3）
上式稱為斯托克斯公式，式中的η為流體的粘性係數、r為球形物體的半徑。
在理論力學中所說的”與物體速度一次方成正比的阻力”，指的就是粘滯阻力。在空氣中運動速度不十分快的物體，受到的阻力主要是粘滯阻力。
粘滯係數
1.流體的動力粘度μ
流體的動力粘度μ，是流體的重要物理屬性，和流體的種類、溫度、壓強有關，在一定的溫度、壓強之下保持常數，其單位為Pa·s。
2.流體的運動粘度
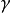
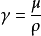
運動粘度只是動力粘度和密度的一個比值，不是流體的固有物理屬性，不能用來比較流體間的粘度大小。
影響粘度因素
壓強
壓強改變對氣體和液體粘性的影響有所不同。由於壓強變化對分子的動量交換影響非常微弱，所以氣體的粘性隨壓強的變化很小。壓強增大時對分子的間距影響明顯，故液體的粘度受壓強變化的影響較氣體大。
液體動力粘度隨壓強變化可以用經驗公式計算：
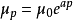
µp——壓強為p時的動力粘度，Pa·s；
µ0——一個大氣壓時的動力粘度，Pa·s；
a——與液體的物理性質、溫度有關的係數，通常近似取，（2～3）×10-8，1/Pa。
溫度
溫度對液體和氣體粘度的影響截然相反，溫度升高時氣體分子的熱運動加劇，氣體的粘度增大，分子距增大對氣體粘度的影響可以忽略不計。對於液體，由於溫度升高體積膨脹，分子距增大，分子間的引力減小，故液體的粘性隨溫度升高而減小，而液體溫度升高引起的液體分子的熱運動量的變化對粘度的影響可以忽略不計。
工程中常用的機械油的動力粘度和溫度之間的變化關係，在20℃～80℃的範圍內可用下式計算：
µt——溫度為t 時的動力粘度，Pa·s；
µ0——溫度為0時的動力粘度，Pa·s；
θ——粘溫係數，對於礦物機械油可取，θ=（1.8～3.6）×10-3，1/℃。
水的動力粘度隨溫度的變化關係可用下式計算：
µt——溫度為t 時的動力粘度，Pa·s；
µ0——水在0℃時的動力粘度，Pa·s；
氣體的動力粘度在低於10個大氣壓時可用蘇士蘭關係式計算：
µt——溫度為t 時的動力粘度，Pa·s；
µ0——氣體在0℃時的動力粘度，Pa·s；
S——按氣體種類確定的常數，K，對於空氣常取S=111K。
溫度（℃） | µ×10-6（Pa·s） | ν×10-6（m2/s） | 溫度（℃） | µ×10-6 （Pa·s） | ν×10-6 （m2/s） |
0 | 17.09 | 13.20 | 120 | 22.60 | 25.20 |
20 | 18.08 | 15.00 | 140 | 23.44 | 27.40 |
40 | 19.04 | 16.90 | 160 | 24.25 | 29.80 |
60 | 19.97 | 18.80 | 180 | 25.05 | 32.20 |
80 | 20.88 | 20.90 | 200 | 25.82 | 34.60 |
100 | 21.75 | 23.00 | 240 | 27.33 | 39.70 |
