粗差

粗差是指在相同觀測條件下作一系列的觀測，是測量誤差的種類之一，一般是指絕對值大於3倍中誤差的觀測誤差，包括內外業中因疏忽大意而造成的差錯在內。其絕對值超過限差的測量偏差，含有粗差的測量數據絕不能採用。

基本介紹

• 中文名：粗差
• 外文名：gross error
• 性質：測量誤差
• 特徵：在相同觀測條件下作一系列的觀測
• 測量條件：應保持觀測時間內條件一致
• 探測準則：萊特準則、格拉布斯準則等

術語簡介

粗差為由於觀測者的疏忽所造成的錯誤結果或超限的誤差。例如瞄錯觀測目標、讀數錯誤和記錄錯誤等。粗差的存在將大大影響平差結果的可靠性，甚至導致完全錯誤的結果。

野外測繪

傳統上是在進行測量外業和內業的過程中，通過一系列的措施，例如採用適當的觀測程式，進行可供檢核的重複觀測，增加多餘觀測，利用幾何條件的閉合差大小加以限制等，及時發現並限制粗差，發現後予以剔除。

儘管如此，仍然難免會有殘存的小粗差存在。因此，從20世紀60年代末起，又相繼發展了一些處理粗差的理論和方法，其中有以統計假設檢驗為基礎的粗差檢驗法，如荷蘭巴爾達(Baarda，W.)教授提出的數據探測法等，此外還有以穩健估計為基礎的選權疊代法等，從而在平差計算中實現了粗差自動剔除的目的。

粗差來源

粗差主要由測量過程中某些意外事件或者不確定的意外因素所引起。從測量誤差來源分析，可將粗差的來源歸為以下3個方面。

誤差分布

外界條件

在測量過程中，由於外界條件的干擾、外界條件的突變、測量狀態的瞬間改變等因素產生的粗差。

測量儀器

測量儀器本身存在缺陷，使用前未經檢驗，或者測量儀器某些部件的偶然失效等因素引起的測量粗差。

人為因素

由於測量人員的疏忽、麻痹大意等出現讀數錯誤、記錄錯誤、測量錯誤、計算錯誤等，或者工作責任心不強、過度疲勞、缺乏經驗、操作不當等。這些均是由於人為的因素所造成的粗差。

粗差檢測

選權疊代法

選權疊代法是把含粗差的測量觀測值看作選自相同期望異常大的方差母體的子樣本，它的基本思想是先用最小二乘方法進行平差，得到第一組的殘差，在每一次經過平差處理後，依據計算出的殘差和與之相關的其它部分參數，按照事先選取的權函式，推導出下一次計算中觀測數據的相對應的權。

最總，包含粗差的那段路線的觀測數據的權將會越來越小，直到最後趨於零。選權疊代法的權函式的選取有各種各樣形式，比較常用的方法也很多，主要有：Huber 法 和IGG法。

數據探測法

數據探測法中只介紹檢驗法。有時，在某些情況下，無法事先知道測量數據母體方差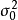值的大小，所以Pope 提出使用剔除測量觀測值之前計算求出的方差估值來替換 促成統計量：

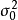
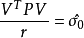
並說明在原假設觀測數據不存在超限誤差情況下，統計量將服從自由度值為r 的分布，因此可以使用機率式：

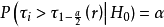
對原假設進行檢驗，這一檢驗方法通常稱為 檢驗法。

數據探測法和選權疊代法在對粗差進行檢驗時有很大的區別：數據探測法是把粗差歸入函式模型時的粗差探測方法，而選權疊代法是把粗差歸入隨機模型時的粗差探測方法。

處理要求

粗差產生的最普遍原因是觀測時的儀器精度達不到要求、技術規格的設計和觀測程式不合理，以及觀測者粗心大意和儀器故障或技術上的疏忽等。粗差是指觀測值中離群較大的誤差，它不同於偶然誤差，一般只是少數，在進行參數估計時，應首先將粗差剔除。

測繪儀器

為了避免粗差的出現，需要：

①提高觀測人員的責任感，仔細檢查所照準的目標；

②再次照準及讀數以檢查觀測值的一致性；

③記錄員回報觀測數據；

④計算校核等，必須制定有效的操作程式和檢核方法去發現並將其剔除。

粗差特點

數量少

在一組等精度觀測的數據中，含有粗差的數據一般很少。如果觀測數據中不包含粗差和系統誤差，則誤差就只有偶然誤差。根據偶然誤差的特性，其值具有有界性。也就是說，含有粗差的異常數據殘差超過3倍中誤差的可能性非常小。從統計學角度來看，這是一個小機率事件，發生的可能性很小。

突發性強

引起粗差的因素很多，有些可以預見，而有些則無法預見，具有突發性的特點，如測量儀器的突發故障、測量人員的偶然失誤等。因此，粗差的產生具有突發性，既不遵循規律，也無規律可循。粗差和偶然誤差不同，所以，粗差也不遵循偶然誤差的統計分布規律。

數值大

測量數據中含有粗差的數據，除非有確定的理由確定其為異常值外，其在統計上一般表現為殘差絕對值很大。如我們對某一量進行等精度觀測時，如果其中某個數值含有粗差，那么它的殘差就會表現為比其他數據的殘差偏大。

套用與意義

測量數據處理是測量工作中必不可少的一項內容，也是測量成果獲取的關鍵步驟，測量數據處理精度的高低直接關係到測量成果的可靠性，因此，測量數據處理是測繪科學的重要組成部分。

近些年，隨著測繪科學的發展，各種新方法、新儀器的湧現，使得測量數據處理髮生了很多變化，原有的理論和方法不斷被改進，新的數學方法也不斷被引進測量領域，這使得測量數據處理理論得到了極大的發展和擴充。

測繪儀器

比如，變形監測數據處理方面，傳統的基於平差的數據處理方法已成為經典，而像灰色系統理論、人工神經網路理論、小波理論等新引入測量領域的數據處理方法在變形監測領域得到了非常廣泛的套用。這些變化為我們的測量工作提供了更高的精度和效率，但也對我們的技術人員提出了更高的要求。

但是，不管測量技術如何發展，數據處理方法如何擴展，測量數據中含有粗差是一件不可避免的事情，對其探測與處理一直是測量數據中的重要工作之一。

測量觀測中，除了含有系統誤差與偶然誤差外，經常還有混進的粗差，如果不對這些粗差予以剔除而直接進行平差，勢必會影響平差的質量和結果。

因此，從觀測數據中探測與剔除粗差就成為了測量數據處理中一個非常重要的問題。各種粗差處理也具有重要的意義。