基本介紹
- 中文名:簡單路徑
- 外文名:Simple path
- 所屬學科:數學
- 相關概念:圖,路徑等
圖論中的簡單路徑,定義,相關概念,Rn中的弧,
圖論中的簡單路徑
定義
如果路徑上的各頂點均不互相重複,稱這樣的路徑為簡單路徑。如果路徑上的第一個頂點與最後一個頂點重合,這樣的路徑稱為迴路(cycle)或環或圈。如在圖1中,迴路有

 圖1
圖1相關概念
圖結構是由有限非空頂點集合V和邊集合E組成的一種數據結構。記作 。頂點具有數據元素,邊表示任意兩個頂點
。頂點具有數據元素,邊表示任意兩個頂點 和
和 之間的關係,記作
之間的關係,記作 。若圖G中
。若圖G中 與
與 不等價,則稱G為有向圖;若
不等價,則稱G為有向圖;若 與
與 等價,則稱G為無向圖,並以無序對
等價,則稱G為無向圖,並以無序對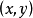 代替兩個有序對
代替兩個有序對 和
和 。圖中每條邊可以有一個稱為權的數與之相連,權可以表示兩個頂點之間的距離或從一個頂點到另一個頂點的代價,這種帶權的圖通常稱為網。
。圖中每條邊可以有一個稱為權的數與之相連,權可以表示兩個頂點之間的距離或從一個頂點到另一個頂點的代價,這種帶權的圖通常稱為網。








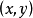


圖 中,從頂點
中,從頂點 到頂點
到頂點 的路徑為一頂點序列
的路徑為一頂點序列 ,其中
,其中 。路徑上的頂點都不相同的路徑稱為簡單路徑。第一個頂點與最後一個頂點相同的路徑稱為迴路或環。除了第一個頂點與最後一個頂點外,其餘頂點都不重複的迴路,稱為簡單迴路。若從頂點
。路徑上的頂點都不相同的路徑稱為簡單路徑。第一個頂點與最後一個頂點相同的路徑稱為迴路或環。除了第一個頂點與最後一個頂點外,其餘頂點都不重複的迴路,稱為簡單迴路。若從頂點 到頂點
到頂點 至少存在一條路徑,則稱
至少存在一條路徑,則稱 和
和 是連通的。若圖中任意兩個頂點都是連通的,則稱為連通圖。
是連通的。若圖中任意兩個頂點都是連通的,則稱為連通圖。









在計算機中,通常採用以下幾種存儲結構來表示圖結構。
(1)數組法。用一個一維數組存儲各頂點的數據信息,用一個二維數組表示的鄰接矩陣表示邊的集合。其中鄰接矩陣A是一個n階方陣(n為圖中頂點的個數)。
除以上兩種常用表示法外,還有二進制向量表示法、鄰接多重表和十字鍊表等表示方法。
圖的基本操作有查找、插入和刪除,以及求兩個頂點間的路徑及路徑長度、圖的遍歷和求連線於某一頂點的邊數等。
Rn中的弧
Rn中的弧(arc in Rn)亦稱簡單弧,是曲線弧概念的推廣,它有兩種不同的定義,一種定義是指連續的單射 (這樣,弧是特殊的路徑);另一種定義是指這樣的
(這樣,弧是特殊的路徑);另一種定義是指這樣的 的值域
的值域 。後一種定義更具幾何含義,按照它,弧是自身不相交的曲線,或曲線上任意兩點間不包含重點的部分。採用這種定義時,又稱為若爾當弧,同時,把前一種定義中的
。後一種定義更具幾何含義,按照它,弧是自身不相交的曲線,或曲線上任意兩點間不包含重點的部分。採用這種定義時,又稱為若爾當弧,同時,把前一種定義中的 稱為簡單路徑。
稱為簡單路徑。






