簡單計數問題是指數學中排列組合套用中的計數問題。數學計數原理中排列組合問題簡單的解決方法,是解決計數問題的基本原則與一般策略。
基本介紹
- 中文名:簡單計數問題
- 外文名:Computational theory
- 套用學科:數學
- 適用領域範圍:高中數學
- 適用領域範圍:高考
- 套用領域:統計計算
基本內容,解題步驟,解決方法,舉例,特殊元素優先法,捆綁法,插空法,調序法,注意事項,
基本內容
排列定義: 一般地,從n個不同元素中取出m (m≤n) 個元素,按照一定的順序排成一列,叫做從 n 個不同元素中取出 m 個元素的一個排列。
組合定義:一般地,從n個不同元素中取出m(m≤n)個元素並成一組,叫做從n個不同元素中取出m個元素的一個組合。
解題步驟
1.把具體問題化歸為排列或組合問題;
2.通過分析確定運用兩個計數原理;
3.分析題目條件,避免重複或遺漏;
4.列出式子,準確計算。
2.通過分析確定運用兩個計數原理;
3.分析題目條件,避免重複或遺漏;
4.列出式子,準確計算。
解決方法
解決計數問題的常用策略有:
(1)特殊元素優先安排:從元素的特殊性上講,對問題中的特殊元素應優先排列,然後在排列其他一般元素;從位置的特殊性上講,對問題中的特殊位置應優先考慮,然後再排其他剩餘位置。
(2)相鄰問題捆綁處理(先整體後局部):在解決對於某幾個元素要求相鄰的問題時,先整體考慮,將相鄰元素視作一個大元素進行排序,然後再考慮大元素內部各元素間順序的解題策略就是捆綁法。
(3)不相鄰問題插空處理:"不鄰問題"插空法,即在解決對於某幾個元素要求不相鄰的問題時,先將其它元素排好,再將指定的不相鄰的元素插入已排好元素的間隙或兩端位置,從而將問題解決的策略。
(4)順序一定問題除法處理:當某些元素次序一定時,可用調序法。先將n個元素進行全排列 種,m(m<n)個元素的全排列有
種,m(m<n)個元素的全排列有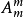 種,由於要求m個元素次序一定,因此只能取其中的某一種排法,可以利用除法起到調序的作用,即若n個元素排成一列,其中m個元素次序一定,共有
種,由於要求m個元素次序一定,因此只能取其中的某一種排法,可以利用除法起到調序的作用,即若n個元素排成一列,其中m個元素次序一定,共有 種排法。
種排法。

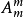

舉例
特殊元素優先法
例1.用0,2,3,4,5這五個數字,組成沒有重複數字的三位數,其中偶數共有()個。
解:因組成的三位數為偶數,個位的數字必須是偶數,又0不能排在首位,故0是其中的“特殊”元素,應優先安排,按0排在個位和0不排在個位分為兩類:①當0排在個位時,有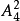 個;②當0不排在個位時,三位偶數有
個;②當0不排在個位時,三位偶數有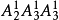 個。由分類加法計數原理,其中偶數共有30個。
個。由分類加法計數原理,其中偶數共有30個。
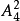
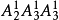
捆綁法
例2.從單詞“equation”中選取5個不同的字母排成一排,含有“qu”(其中“qu”相連且順序不變)的不同排列共有( )種。
解:先將“qu”看成一個元素,再從剩餘的6個元素中取出3個元素,共有 種不同取法,然後對取出的4個元素進行全排列,有
種不同取法,然後對取出的4個元素進行全排列,有 種方法,由於“qu”順序不變,根據分步乘法計數原理共有
種方法,由於“qu”順序不變,根據分步乘法計數原理共有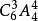 =480種不同排列.
=480種不同排列.


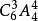
插空法
例3.要為5名志願者和他們幫助的2位老人拍照,要求排成一排,2位老人不相鄰且不排在兩端,不同的排法共有()種。
解:先排五名志願者,兩位老人插空。5名志願者的排法有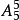 種,2位老人不相鄰且不排在兩端,採用插空,中間四個空,有
種,2位老人不相鄰且不排在兩端,採用插空,中間四個空,有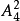 種,由分步乘法計數原理共有
種,由分步乘法計數原理共有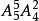 =1 440種。
=1 440種。
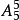
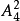
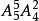
調序法
例4.由數字0,1,2,3,4,5組成沒有重複數字的六位數,其中個位數字小於十位數字的共有()個。
解:若不考慮附加條件,組成的六位數共有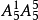 個,而其中個位數字與十位數字的
個,而其中個位數字與十位數字的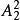 種排法中只有一種符合條件,故符合條件的六位數共有
種排法中只有一種符合條件,故符合條件的六位數共有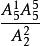 =300個。
=300個。
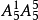
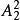
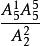
注意事項
解決排列組合綜合問題,應遵循三大原則:先特殊後一般,先分組後排列,先分類後分步的原則。充分考慮元素的性質,進行合理的分類和分步,尋找並理解“關鍵字”的含義及其等價問題。

