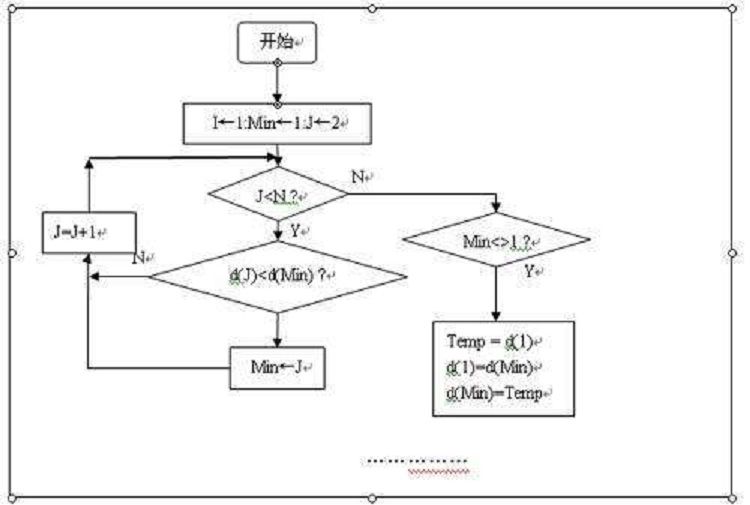
基本介紹
- 中文名：範圍最值查詢
- 外文名：Range Minimum Query
- 類型：一種查詢算法
簡介,ST算法,
簡介
若
，條件為
的範圍最值查詢返回1，它是子數組
中最小的元素。
通常情況下，數組A是靜態的，即元素不會變化，例如插入、刪除和修改等，而所有的查詢是以離線的方式給出的，即預先並不知道所有查詢的參數。在上述條件下，將數組以特定方式進行預處理即可以使範圍最值查詢在常數時間內得到處理。
現有算法可以通過以線性時間
對數組進行預處理以獲得之後常數時間的範圍最值查詢處理，其空間複雜度為。範圍最值查詢問題（RMQ）與最低公共祖先（LCA）問題有直接聯繫，它們可以互相轉化。RMQ的算法常常套用在嚴格或者近似子串匹配等問題的處理中。
RMQ問題的常見解決方法有線段樹、ST(倍增)、排序和樸素。
樸素算法就是每次查詢都For一遍，時間複雜度
。排序法就是新開一個數組記錄數的位置，排序後每次查詢從頭到尾For一遍，找到第一個在區間中的數退出即可。編程複雜度低，但是實際效果可能並不好。最壞情況時間複雜度
，但平均情況會比樸素快那么一點。倍增法請參見下面部分。線段樹是最快的算法，但是編程複雜度非常高，因此除非數據很大極少使用。
ST算法
建立一個二維數組
的整數值。
在這個數組中
表示範圍
中的最大值（例如
中的最大值被計為
）。
建立數組的過程可以在
時間內完成。具體算法類似於動態規劃。以下是C++語言描述的代碼，數組約定從0開始：
void Initialise(vector<int> &Array){int Length = (int)Array.size(); // 長度為 0 時，表示數據自身。for (int i = 0; i < Length; ++i) F[i][0] = Array[i];for (int j = 1; (1 << j) <= Length; ++j)for (int i = 0; i + (1 << j) - 1 < Length; ++i)F[i][j] = min(F[i][j - 1], F[i + (1 << (j - 1))][j - 1]); // 分成長度相等的兩段}當我們需要計算一個區間中的最大值（例如
時），我們先求出這個區間的長度（即 8-3+1=6）。
然後我們算出不大於它的最大
值的指數（即2）。我們要查詢分別以3開頭，和以8結尾的兩個長度為
的區間的最大值。
顯然
和
也就是（
和
）的最大值就是的最大值。查詢的時間是常數，代碼如下：
int Query(int Left, int Right){int i = 0;while (1 << (i + 1) <= Right - Left + 1) ++i;return min(F[Left][i], F[Right - (1 << i) + 1][i]);}整個程式的時間複雜度是
，Q為查詢數。
