有特殊計算方法的行列式的一種。
除第一行、第一列及主對角線外的元素都是0的行列式。
基本介紹
- 中文名:箭形行列式;箭型行列式;爪形行列式
- 外文名:arrow determinant
- 所屬學科:線性代數
定義
學科特點
套用
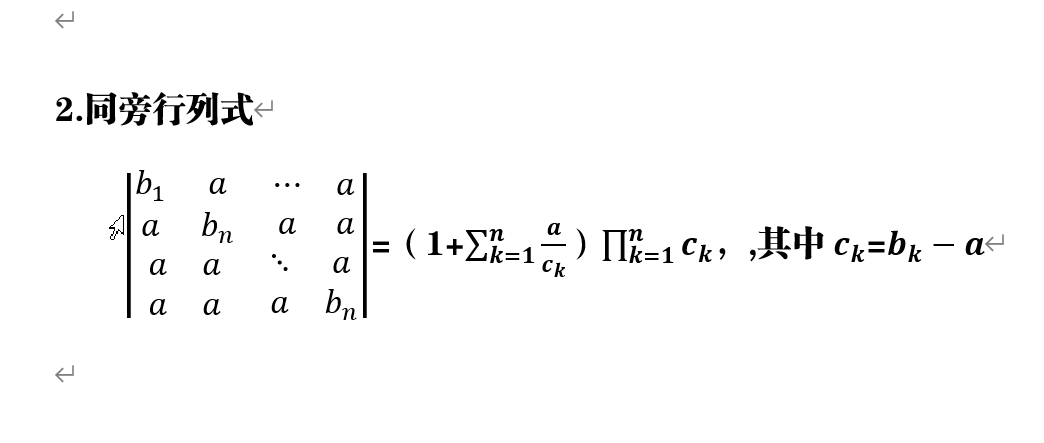
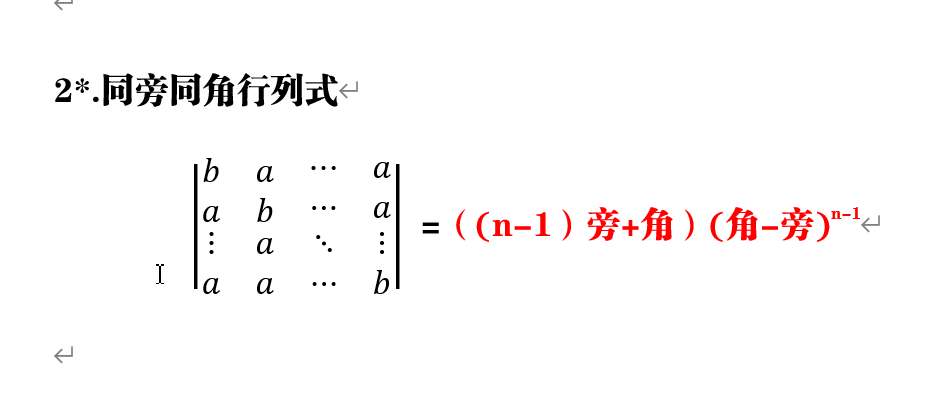

有特殊計算方法的行列式的一種。
除第一行、第一列及主對角線外的元素都是0的行列式。
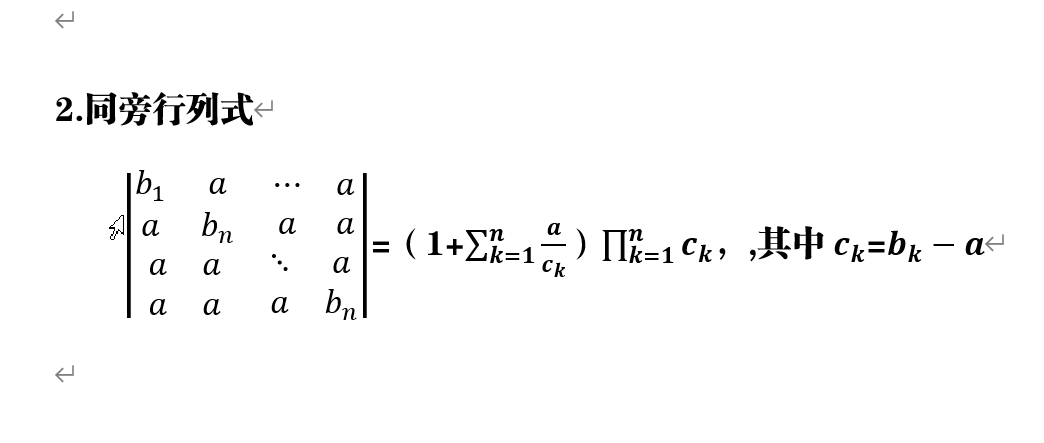

有特殊計算方法的行列式的一種。除第一行、第一列及主對角線外的元素都是0的行列式。定義除第一行、第一列及主對角線外的元都是0的行列式學科特點可化為上三角行列式求值套用箭形行列式有兩種常見的變形:同三角行列式,同三角同對角元...
1.6利用初等變換化為三角行列式來計算行列式 1.7箭形行列式 1.8-三對角行列式 1.9分塊的三角行列式 1.10按行按列展開計算餘子式的代數和 1.11伴隨矩陣的行列式 1.12-方陣乘積的行列式 1.13克萊姆法則 第二章 矩陣代數 2.1伴隨矩陣 2.2矩陣方程 2.3-方陣的冪 2.4-向量的內積與外積 2.5方陣可逆的...
第二章 行列式 2.1 知識脈絡圖解 2.2 重點、難點解讀 2.3 典型例題解析 2.3.1 逆序數與行列式定義 2.3.2 可直接利用性質計算的行列式 2.3.3 兩條線型行列式的計算 2.3.4 箭形行列式的計算 2.3.5 三對解行列式的計算 2.3.6 Hessenberg型行列式的計算 2.3.7 計算行(列)和相等的行列式 2.3....
第1講 行列式 1.1 本講內容聚焦 一、內容要點精講 二、知識結構圖解 三、重點與難點解讀 四、考試內容與要求 1.2 典型例題分類解析 一、逆序數與行列式定義 二、可直接利用性質計算的行列式 三、兩條線型行列式的計算 四、箭形行列式的計算 五、三對角行列式的計算 六、Hessenberg型行列式的計算 七、計算行(...
線性代數部分以矩陣及其運算為主線,把行列式看作矩陣的一個數值特性,突出矩陣的三個數值特性(行列式、秩和特徵值)線上性代數中的作用,將向量組“線性方程組”二次型及線性變換與矩陣建立聯繫,重點對矩陣進行研究,然後用矩陣理論來解決相關問題。將初等變換作為線性代數的主要計算工具。該書中求矩陣的逆、行列式、...
