等待時間(waiting time)指等待制服務系統中,呼叫因不能立即得到服務而在系統內排隊等待服務的時間。它在數值上等於從呼叫發生到呼叫開始被服務的這段時間長度。
基本介紹
- 中文名:等待時間
- 外文名:waiting time
概述
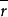
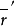
數學模型
 圖1 愛爾蘭全利用度等待系統模型
圖1 愛爾蘭全利用度等待系統模型 圖2 三節點網
圖2 三節點網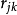


等待時間(waiting time)指等待制服務系統中,呼叫因不能立即得到服務而在系統內排隊等待服務的時間。它在數值上等於從呼叫發生到呼叫開始被服務的這段時間長度。
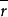
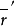
 圖1 愛爾蘭全利用度等待系統模型
圖1 愛爾蘭全利用度等待系統模型 圖2 三節點網
圖2 三節點網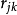


等待時間(waiting time)指等待制服務系統中,呼叫因不能立即得到服務而在系統內排隊等待服務的時間。它在數值上等於從呼叫發生到呼叫開始被服務的這段時間長度。...
平均等待時間是指MO磁光碟機的磁頭已處於要訪問的磁軌,等待所要訪問的扇區旋轉至磁頭下方的時間。...
在網路通信,等待時間是指信號從網路結點傳送到另一網路結點所需要的時間。在計算機中,等待時間有很多解釋,讀寫等待時間就是其中一種,讀寫等待時間是指CPU等待數據...
中國式過馬路和紅燈時長超行人忍耐限度有關,假如行人在等待期間,並且時間超過70秒後,行人就要慢速前進,思索其他位置等候。這70秒,就被叫行人可忍受等待時間。...
Win32 API提供了一組能使執行緒阻塞其自身執行的等待函式。這些函式只有在作為其參數的一個或多個同步對象(見下小節)產生信號時才會返回。在超過規定的等待時間後,...
在計算機網路中,由於不同的通信子網和網路體系結構採用不同的中轉控制方式,在通信子網中存在的中轉延遲是由網路狀態決定的。電信號回響帶來的延遲時間是固定的,回響...
等待效應(Wait effect)由於人們對某事的等待而產生態度、行為等方面的變化,這種現象稱等待效應。在管理中,優秀管理者常常利用這種效應的作用,使員工產生一種對新任務...
《讓時間等候》是楊峰演唱的一首歌曲...... 《讓時間等候》是楊峰演唱的一首歌曲 中文名稱 讓時間等候 [1] 歌曲原唱 楊峰 [1] 目錄 1 歌曲信息 2 歌曲歌...
等待1 作詞:九級旋風(劉海軍) 作曲:冬雪映春(崔秀冬) 編曲:冬雪映春(崔秀冬) 歌詞內容 春去秋又來 落葉滿天飛 在這迷茫的季節 始終不見你回來 時光依舊輪迴...
等待航線(holding pattern)是一種航空術語,指飛機待降時在等待空域的飛行航線。其目的是為了調配飛機的間隔、消失高度、等待天氣的好轉或處理特殊情況等。等待航線...
逗留時間( average time a customer spends in thesystem)排隊系統中從顧客到達時刻起至他接受服務完成止的時間。即顧客在系統中的停留時間,等於等待時間與服務時間...
掛號、劃價、收費、取藥等服務視窗等候時間不超過10分鐘。 衛生部提出,全國所有三級甲等醫院要實行多種方式預約診療,城市社區衛生服務機構轉診預約的優先診療。到...
《等待》是陳綺貞作詞作曲並演唱的歌曲。...... 《等待》是陳綺貞作詞作曲並演唱的歌曲。中文名稱 等待 所屬專輯 還是會寂寞 發行時間 2000年03月 歌曲語言 ...
TDR等待時間是一款大小為1.11MB的套用,適用固件為Android2.1及以上。...... TDR等待時間是一款大小為1.11MB的套用,適用固件為Android2.1及以上。目錄 1 基本信息 ...
《只能等待》是隳迭發表在晉江文學城的小說作品。...... 當時間與空間的距離無法克服 當心與心的交流無法繼續 我們能做的只有等待 等待……詞條標籤: 網路小說 ,...
《等待》是亞細亞之聲黃綺珊主唱的一首國語歌,由汪峰作詞作曲,收錄於專輯《只有你》,喜洋洋唱片於2000年12月1日發行。...
英文:Wait To Restore time 解釋:路徑/連線從故障中恢復之後到能被再次使用以傳輸正常業務信號和/或從中選擇正常業務信號之前所需等待的時間稱為等待恢復時間。 ....
《等待完整》是由梁錦興填詞,黃晟峰譜曲,胡夏演唱的歌曲,該歌曲收錄於2010年12月20日發行的專輯《胡愛夏》中。...
《在等待》是李慧珍第一張專輯,收錄歌曲10首。1997年1月在國內發行,同年5月在日本發行。同名主打歌曲《在等待》獲“中國歌曲總評榜”1997年第一季度12期十大...
《如果時間會等待》是連載於瀟湘書院的小說,作者是琉璃魚。...... 《如果時間會等待》是連載於瀟湘書院的小說,作者是琉璃魚。中文名 如果時間會等待 作者 琉璃魚...
《我還有多久時間來等待》是在晉江文學城連載的原創小說,作者是糖糖魚。...... 《我還有多久時間來等待》是在晉江文學城連載的原創小說,作者是糖糖魚。...
平均訪問時間(Average access time):指磁頭找到指定數據的平均時間,通常是平均尋道時間和平均潛伏時間之和。平均訪問時間最能夠代表硬碟找到某一數據所用的時間,越短...
《等待你的時間》是夢影星創作的網路小說,發表於晉江文學網。...... 《等待你的時間》是夢影星創作的網路小說,發表於晉江文學網。中文名稱 等待你的時間 作者 ...
《等待的意義》由作者靈波微步發布晉江文學城的愛情小說。等待的意義是什麼?等到繁華落盡,思念之情幻化成雲,似乎一切都無法脫出時光的力量。 如果我一直保持緘默,...
《等待您》是中國香港男歌手陳百強的一張音樂專輯,由華納唱片公司於1990年發行,該專輯由10首歌曲組成。...
《等待》是陳可辛執導,章子怡、金城武主演的愛情片。影片講述了一個關於“等待”的故事:與護士有婚外情的軍醫孔林等待了18年,終於與老家的原配妻子離成了婚。...
等待是一首由韓磊演唱,葛根塔娜作詞,張宏光作曲的歌曲,是電視劇《漢武大帝》的片尾曲,該歌曲被收錄於韓磊2005年專輯《帝王之聲》。...
為何那時間不能再回頭 可以讓我重新好好的再把握 啊 漫漫的長夜總是那樣的寂寞...1. 這樣的等候 .百度音樂.2015-05-29[引用日期2015-05-29] V...
《等待的人被時間拋棄》是連載於連城讀書的一本都市類小說,作者是朽木可琢。...... 《等待的人被時間拋棄》是連載於連城讀書的一本都市類小說,作者是朽木可琢。...
排隊論(queuing theory), 或稱隨機服務系統理論, 是通過對服務對象到來及服務時間的統計研究,得出這些數量指標(等待時間、排隊長度、忙期長短等)的統計規律,然後...
