集合A所含元素的個數稱為A的勢(或基數)。
若存在從集合A到集合B的一一對應(雙射),則稱A與B等勢(或對等),記作A~B. 相應地,稱A、B為等勢集(亦稱對等集、等基數集)。
一一對應或對等可用於比較集合的大小(即集合所含元素個數的比較)。空集只與自身對等;兩個有限集對等若且唯若它們的元素個數相同;與自然數集對等的集合稱為可列集或可數集,與實數集對等的集合稱為具有連續勢。
基本介紹
- 中文名:等勢集
- 外文名:equivalent set
- 別名:對等集、等基數集
- 概述:量集合間有一一對應關係
- 相關概念:集合的勢
- 套用領域:集合論
引言,等勢集,勢,可列集,定義,性質,舉例,
引言
給定一個集合X以及某個與X中元素相關的命題 ,令
,令 (註:在這裡,
(註:在這裡, 若且唯若
若且唯若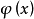 成立),
成立), . 一個有意思的問題是:
. 一個有意思的問題是: 在X上成立與不成立的可能性哪個更大?這涉及集合A與B所含元素的個數的比較。
在X上成立與不成立的可能性哪個更大?這涉及集合A與B所含元素的個數的比較。



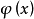


對於有限集,這個問題的解決是簡單的,只要比較集合A與B中所含元素個數就行了。對於無窮集,個數一詞沒有實際意義。然而,不同的無窮集,它們是有明顯的差別的。比如自然數集與實數集顯然不同。自覺上,實數當然比自然數多得多。那么怎樣表示集合所含元素的多少呢?怎樣比較兩個無窮集所含元素的多少呢?對於兩個有限集合是否有相同的元素個數,只需要看能否在兩個集合之間建立一種一一對應關係。這種方法可推廣到無窮集。
等勢集
定義1(對等)設A,B是兩個集合,如果存在一個從A到B的一一滿映射(雙射),則稱集合A與B對等(也可稱A與B是等勢集,或A與B之間有一一對應關係),記作

顯然對等關係滿足如下性質:
(1)自反性:

(2)對稱性:若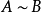 ,則
,則
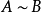

(3)傳遞性:若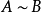 ,
, ,則
,則
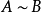


任何滿足自反性、對稱性和傳遞性的二元關係稱為等價關係。於是集合的對等關係是一種等價關係。
例1 N~Z.作對等關係如下:


例2 在對等關係 下,有(-1,1)~R. 即集合(-1,1)與實數集R是等勢集。
下,有(-1,1)~R. 即集合(-1,1)與實數集R是等勢集。

勢
定義2(集合的勢)設A,B是兩個集合,如果 ,就稱A與B有相同的勢(或基數)。記|A|為集合A的勢(或基數)。
,就稱A與B有相同的勢(或基數)。記|A|為集合A的勢(或基數)。

註:(1)若存在一個從A到B的一一映射(相當於A對等於B的一個子集),則稱 如果
如果 ,則稱
,則稱 (讀作|A|小於|B|).
(讀作|A|小於|B|).



顯然,若 ,則
,則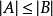 ;若存在滿映射
;若存在滿映射 ,則
,則

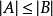


(2)若A是含n個元素的有限集,則記|A|=n;對於無限集A,通常也用一個希臘字母如α記|A|,且形象地說“A含有α個元素”。當|A|<|B|時,可以說“B含有比A更多的元素”。
(3)對於任意兩個勢α、β,關係式α<β,α=β,β<α中有且僅有一式成立。
(4)若α≤β,β≤α,則α=β.
可列集
定義
定義3(可列集)自然數集的勢記為 (讀成阿列夫(Aleph)零),即
(讀成阿列夫(Aleph)零),即 與自然數集對等的集合稱為可列集或可數集。
與自然數集對等的集合稱為可列集或可數集。


集合A為可列集,是指A與自然數集對等,即有一一對應關係 ,於是A={x1,x2,...,xn,...},即A可按順序排成一序列。反過來一個集合可以排成一序列,它便是可列集。
,於是A={x1,x2,...,xn,...},即A可按順序排成一序列。反過來一個集合可以排成一序列,它便是可列集。

性質
可列集具有以下性質:
- 任何無窮集合都包含一個可列子集。
- 可列集是勢最小的無窮集合,它是最簡單的無窮集合。
- 可列集合的無窮子集仍是可列的。
- 設A是可列集,B是有限集或可列集,則A∩B是可列集。
- 可數個有限集或可列集的並仍是可列集。
- 有限個可列集的直積仍為可列集。
- 設集合A的勢為α,則|2A|=2α.
- 設A是無限集,|A|=α,若B是可列集,則|A∪B|=α.
- 集合A是無限集的充分必要條件是:A與其自身的一個真子集對等。
- 區間(0,1)={x|0<x<1}不是可列集。
- 2N~R,即2|N|=c.(與實數集R對等的集合稱為具有連續勢,記為c,即|R|=c.)
- (無最大基數定理)若A是非空集合,則集合A與其冪集2A不對等。
舉例
整數集、有理數集、由有限個自然數構成的有序數組的全體構成的集合、有理係數多項式之全體構成的集合等都是可列集。
證明:
(1)整數集:由例1知N~Z,故整數集Z是可列集。
(2)有理數集:由滿映射


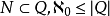

(3)由有限個自然數構成的有序數組的全體構成的集合:記此集合為A,A={(n1,n2,...,nk)|ni∈N,i=1,2,...,k,k∈N}=∪k=1,2,...Nk,其中,Nk={(n1,n2,...,nk)|ni∈N,i=1,2,...,k}. 由上述性質6可得|N|=|N|= ,再由性質5可知A是可列集。
,再由性質5可知A是可列集。

(4)有理係數多項式之全體構成的集合:每個有理係數多項式 由n+1個有理係數
由n+1個有理係數 唯一決定,於是有理係數多項式之全體與有限個有理數構成的有序數組全體構成的集合對等,後者是
唯一決定,於是有理係數多項式之全體與有限個有理數構成的有序數組全體構成的集合對等,後者是 ,與上面的(3)一樣,它也是可列集。
,與上面的(3)一樣,它也是可列集。




