概念
非相對論電子注中的空間電荷波理論,已經詳細地研究過。空間電荷波理論不僅能清晰地描述電磁擾動在電子注中傳播的物理過程,而且可以用於建立各種電子與波互作用機理的線性理論,因此,有極重要的理論與實用價值。非相對論空間電荷波的理論,曾大大地推動了普通
微波管及在非相對論條件下電子與波互作用機理研究的發展,我們相信,相對論空間電荷波理論系統的建立,也必將對相對論電子學的發展重要的推動作用。
無引導磁場電子流的空間電荷波
研究背景
空間電荷波理論不僅能清晰地描述電磁擾動在電子注中傳播的物理過程,而且可以用於建立各種電子與波的互作用機理的線性理論,因此,有極重要的理論和實用價值。傳統的空間電荷波理論均是討論真空中電子注的傳遞,隨著高功率微波技術的發展,
電漿被引人
微波器件中,電漿的引人使微波管中的物理過程變得異常複雜,甚至在某些管中,由於電漿的中和作用,利用電子注的磁自聚焦力,可實現電子注的無磁場聚束傳輸。電漿中的波動過程已有人研究過,但在該環境下傳輸的電子注中傳遞的空間電荷波還未見報導。電漿通道中的電子注,由於其傳輸特性與真空下大不一樣,因而,在其上傳播的空間電荷波亦有其自身的特性,詳細地研究這種空間電荷波無疑對研製和開發電漿微波器件有重要意義。
空間電荷波波動方程
在圓柱坐標系(r,
,z)中,設電子注運動方向為z向,各擾動量有波動因子
形式,對Maxwell方程組進行處理並取
波動方程交流部分的z分量,則
式中:
是自由空間波數,E
1z和J
1z分別為電場矢量和電流密度矢量的Z向交變分量,ρ
1為電荷密度的交變分量。在小信號條件下,假定高頻擾動只使電子偏離平衡位置作微擾運動,則電子坐標可表示為:
其中r
0、z
0為未擾運動坐標,r
1和z
1亦具有
形式。
空間電荷波方程的解
對於空間電荷波方程,首先考慮自磁場可忽略的情況。假定電子注和
電漿均充滿整個空間,由於填充電漿的中和作用,相當於空間電荷力和密度下降,從而即使是一維情況,電漿頻率也下降。R為電漿頻率降低因子,可以證明R遠遠小於1。可見在填充電漿條件下,R變得非常複雜,與電漿中和因子有關。在空間電荷波的研究中,電漿頻率降低是一個重要的參數,真空磁約束下,該量主要與特徵值有關,在電漿約束下,不僅與特徵值有關,而且與電漿填充有關。這為用電漿控制空間電荷波提供了基礎。
由於電漿的加入,空間電位發了變化,表達式雖不變,但與真空條件相比,其值已發生變化。由於空間電荷力的減弱,與真空對比,動電壓值有所提高,動功率流定律形式不變。
主動空間試驗中空間電荷波向電磁波的轉換
研究背景
在主動空間試驗(Active space experiment)中,
電子束和空間
電漿相互作用一直是研究重點之一,利用電子束激發電磁波輻射因其獨特的套用價值而備受關注。從20世紀60年代開始,陸續開展了一系列從空間
飛行器發射電子束的主動空間試驗,其中首次主動發射電子束試驗(“Flash-1”和“Flash-2”) 便觀測到了很強的無線電波輻射,其原因正是電漿和電子束的相互作用。1975年“Araks”試驗分別進行了代號為“North”和“South”的兩次電子束髮射,在電子束入射裝置開啟和關閉時觀測到明顯的電磁波輻射。20世紀90年代開展的“APEX(Active Plasma Experiment)”試驗主要研究電子束侵入低電離層區域產生的人造極光、衛星附近電漿和電子束的相互作用以及電漿高頻波振盪、衛星電荷中和的動力學過程等,試驗過程中觀測到包括哨聲波和高頻波的多頻段波輻射。從已經開展的相關空間試驗來看,對試驗結果的解釋異常複雜,有必要對電子束和空間電漿相互作用激發
電磁波的物理本質進行深入研究。
為此,眾多科研人員做了大量工作。1965年Fainberg首先提出利用調製電子束穿越緻密電漿傳輸電磁波,在實驗室條件下,利用電子束作為電磁波輻射源產生的波輻射已被觀測到。Rogashkova的工作表明,在非均勻冷電漿填充的波導中調製電子束可以激發出電磁波,而且電磁波輻射強度取決於電子束相對於電漿粒子濃度梯度的運動方向,電子束流中空間電荷波的弛豫和電磁波的輻射特性與電漿粒子濃度梯度有關。Krafft進行了有關電子束(包括調製電子束)和電漿相互作用的試驗研究,通過實驗室模擬空間試驗條件,證實了電子束在電漿中激勵哨聲波的兩種機制:切倫柯夫共振輻射和在電子束入射點產生的渡越輻射,並從理論上給予了解釋。Anisimov對基於渡越輻射調製電子束和電漿相互作用產生電磁波輻射以及影響輻射強度的各種因素分別進行了分析,引入了各向異性電漿中渡越輻射形成區域橫向尺度概念,並結合典型的主動空間試驗參數計算了橫向尺度大小,通常可達數十至數百米。在我們早期工作中開展了調製電子束在電離層中激發哨聲波和高頻波輻射的數值計算工作。
空間電荷波轉換係數的理論推導
試驗和理論計算表明,從空間
飛行器入射進
電離層的電子束和電漿相互作用,電子束流中的空間電荷波將轉換為電磁波輻射。前面假設空間電漿是均勻的,在這種情況下渡越輻射不可能發生,當電子束穿越電漿濃度躍變區域時,渡越輻射就會出現。在主動空間試驗中,這樣的電漿密度躍變區域不難找到,電子束入射裝置附近的電漿可滿足該條件。完整求解空間電荷波轉換為電磁波的係數很困難,下面分別就弱磁場近似、哨聲波激發和低頻近似三種典型情況分別計算空間電荷波向電磁波轉換的係數。計算過程中假設兩種電漿交界處粒子濃度發生變化區域的橫向尺度(假設為F)遠小於電漿-束系統中的任意波長。在具體試驗中,這一條件很難滿足,在數值計算過程中之所以做這樣的假設,是因為對於較大尺度的非均勻電漿區域,可以將其劃分為分段區域,每個分段
電漿濃度變化區域的橫向尺度可以滿足上述條件。
假定背景
電漿濃度在
電子束入射裝置處(z=0)發生
躍變:在z <0區域 n
p(z)=n
p1,在z >0區域 n
p(z)=n
p2。考慮到離子濃度的影響,z =0 平面兩側的電漿可以視為準中性,兩側區域的本徵振動都由方程組描述,地磁場方向垂直於電漿邊界。研究電子束從z<0區域入射進z>0電漿區域後電子束的空間電荷波向電漿特徵波的轉換。假定入射波位於 y-z 平面內,在y方向上等離子是均勻的,所以入射波在電漿中激起的波對y的依賴關係和入射波相同。運用
電磁場分量的一般邊界條件和電子速度矢量各分量的連續性條件可以求解在電漿濃度躍變區域空間電荷波轉換為尋常波和非尋常波的係數T
k(k =1,2,3,4)。
數值計算和討論
作為驗證,藉助前期工作的數值計算方法,求解一種典型空間試驗條件下調製
電子束產生的哨聲波輻射。當不考慮電子束弛豫特性時,對應哨聲波頻段,求解各向異性均勻空間電漿的色散方程可得到兩組解,分別對應尋常波模和非尋常波模。對應非尋常波模色散方程的根為純
虛數,它所代表的
電磁波在電漿中將以指數形式很快衰減。對於尋常波模,計算所得電子束激發的哨聲波前向輻射振幅大於後向輻射振幅。當不考慮電子束弛豫時,前向和後向渡越輻射以及前向切倫柯夫輻射方向圖近乎一樣。圖1給出了滿足哨聲波輻射條件時前向輻射方向圖。圖1a中的峰值對應電子束在電漿中滿足切倫柯夫諧振條件時所產生的哨聲波輻射總功率。對於非相對論電子束,後向輻射強度隨著電子束速度的增加而增加。圖1b是電子束弛豫長度為圖1a中電子束弛豫長度 4 倍時得到的輻射方向圖。圖1a和1b對應的電子束弛豫長度分別為20m和80m。在其他參數不改變的情況下,適當增大電子束弛豫長度,將在一定程度上增加電子束產生的哨聲波輻射強度,這是因為電子束弛豫長度的增加,將延長束和背景電漿的作用時間,從而增大波輻射強度,同樣由於作用距離的增加,導致輻射方向圖中出現了多個峰值。
 圖 1 不同弛豫長度時電子束在電漿中產生的哨聲波輻射方向圖
圖 1 不同弛豫長度時電子束在電漿中產生的哨聲波輻射方向圖在“APEX”試驗中,觀測到很強的
電磁波輻射,見圖2。從圖中可以看出,當
電子槍開啟時,觀測結果中出現了明顯的電磁波輻射,當電子槍關閉後,波輻射現象也隨之消失,在電子槍工作過程中一直存在著不同強度的多頻段波輻射。當電子束從電子槍入射進空間
電漿時,在太空飛行器表面和空間電漿的交界區域背景電漿濃度存在著一個躍變,電子束與空間電漿相互作用,電子束空間電荷波轉換為較強的電磁波輻射。
 圖2 “APEX”試驗中電子束入射時觀測到的多頻段波輻射結果
圖2 “APEX”試驗中電子束入射時觀測到的多頻段波輻射結果
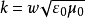

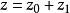

 圖 1 不同弛豫長度時電子束在電漿中產生的哨聲波輻射方向圖
圖 1 不同弛豫長度時電子束在電漿中產生的哨聲波輻射方向圖


 圖2 “APEX”試驗中電子束入射時觀測到的多頻段波輻射結果
圖2 “APEX”試驗中電子束入射時觀測到的多頻段波輻射結果