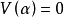晶體內部結構中全部對稱要素的集合稱為 “空間群” 。具體地說是晶胞中全部對稱要素的組合。
基本介紹
簡介,點陣平移,空間群的確定,空間群的三要素,空間群的表達,晶體內部結構對稱要素,空間群符號,
簡介
中文名稱：空間群
晶體內部結構中全部對稱要素的集合稱為 “空間群” 。
一切晶體結構中總共只能有230種不同的對稱要素組合方式，即230個空間群。它是由俄國結晶學家費多洛夫和德國結晶學家薛弗利斯（Artur Moritz Schoenflies，1853-1928）於1890至1891年間各自獨立地先後推導得出來的，故亦稱為“230個費多洛夫群”。
空間群可以分為兩類：一類稱為簡單空間群或稱點空間群；一類稱為複雜空間群或稱非點空間群。
所謂點空間群，是由一個平移群和一個點群對稱操作組合而成的，它的一般對稱操作可以寫成（R | t (αβγ)），其中R表示點群對稱操作，t(αβγ)表示平移操作。具體分析表明，共有73種不同的點空間群。
點陣平移
理想的完整晶體應是無限大的，點陣單元在空間三個方向上的無限平移將給出整個點陣。或者說，無限的點陣在平移下保持不變。所以平移也是一種對稱操作，它的對稱要素不是一個軸，一個點，一個面，而是整個點陣。與平移有關的對稱要素有三個：
- 點陣。與其相應的操作是平移；
- 螺旋軸。相應的操作是轉動和平移組成的複合對稱操作。操作進行時，先繞一軸轉動一定角度，然後再沿與此軸平行的方向進行平移（或先平移再轉動），該軸就稱螺旋軸。螺旋軸的軸次也只有1，2，3，4，6。對於n重螺旋軸，沿軸向的平移，因晶體的周期性要求，由公式決定。其中，為軸向上的點陣周期，m是整數，並且 m<n。
- 滑移面。相應的操作是鏡映和平移組成的複合操作。操作進行時，先通過某一平面進行鏡映，然後在與平面平行的方向上平移一定距離，該平面就稱滑移面。
應該注意，與點陣、螺旋軸、滑移面對應的對稱操作，空間上的每一點都移動了，具有這種性質的操作稱空間操作。因為空間操作直接與晶體微觀結構的周期性相聯繫，故也稱微觀對稱操作，其階為
。與空間操作相對應的對稱操作要素只能存在於無限的結構中，而不能存在於有限的晶體中。
包括了這些與平移有關的操作之後，晶體的對稱運動可以全部分類成230個對稱操作群，稱晶體空間群，也稱空間群。
空間群的確定
如果知道了點群和點陣平移以外，還已知非晶格平移矢量
，布拉維格子類型，則空間群就完全確定，列舉出所有可能的α和的相容性組合，就可得到所有可能的空間群。空間群共有230種，其中73種為簡單空間群，餘下的157種為複雜空間群。
空間群的三要素
非晶格平移矢量決定於與轉軸相聯繫的坐標原點的選擇，因此不是唯一的。
確定空間群必須指出的三個組成部分：
- 容許的點陣平移；
- 空間群點群。它是點陣的全對稱群或它的子群；
- 對應點群所有元素的非晶格平移矢量，但對於簡單空間群有。
空間群的表達
空間群需要用一定的符號形式來表達。較廣泛使用的與對稱型的符號一致，共有兩種，即國際符號和聖佛利斯符號。
晶體內部結構對稱要素
- 螺旋軸：國際符號一般寫作ns，若延旋轉軸的方向的節點間距記為T，則ns表示質點相應的最小基轉角α=360°/n（逆時針旋轉），平移距離為t=s/nT；
- 滑移面：按其滑移方向和距離可分為a,b,c,e,n和d六種。其中a,b,c,e為軸向滑移面，a,b,c分別平行X、Y、Z 軸，滑移距離分別為a/2,b/2,c/2。當軸向滑移面能延兩個軸向滑移時，該軸向滑移面成為雙滑移面e。n滑移面叫做對角線滑移面，它的滑移方向是兩個晶軸的角平分線方向，滑移距離為所涉及晶軸軸單位的一半。d滑移面即金剛石滑移面，它的滑移方向是兩個晶軸的角平分線方向（也可以是三個晶軸的角平分線方向），但滑移距離是所涉及晶軸軸單位的1/4。
空間群符號
表示一個空間群時，聖佛利斯符號和國際符號並用。
空間的國際群符號由兩部分組成：前一部分是格子類型（布拉維格子）[P，C(A、B)，I，F]；後一部分與點群的國際符號基本相同，不同的是那三個特定方向上的對稱要素取自晶胞中對應方向上對稱程度最高的那種對稱要素。
空間群的聖佛利斯符號是在其點群聖佛利斯符號的右上角加上序號即可。
