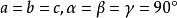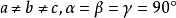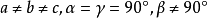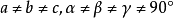基本介紹
空間格子(space lattice)又稱“空間格架”。通常與“空間點陣”視為同義語。是由一系列有規律地在三維空間成周期性重複排列的幾何點(稱為結點)所聯接成的無限的立體幾何圖形。它是從具體的晶體結構中抽象出來的。結點在空間格子中排列的規律性體現了晶體結構中原子、離子或分子在空間分布上的規律性。排列在一條直線上的結點聯接成行列,行列上相鄰結點間的距離稱為結點間距。凡相互平行的行列,其結點間距必定相等。分布在一個平面上的結點則聯接成面網,面網上單位面積內的結點數稱為面網密度,相鄰二平行面網間的距離為面網間距。凡相互平行的面網,其面網密度和面網間距必定全都相同。一個空間格子總是可以被三組相交的面網將整個空間劃分為一系列相互平行疊置的平行六面體而表現為格子狀。如果使所劃分出來的平行六面體既能體現出整個空間格子的對稱性,直角關係儘可能多而體積又為最小,這樣的平行六面體稱為單位平行六面體。根據單位平行六面體對稱性的不同,空間格子分別歸屬於七個晶系;再根據結點在單位平行六面體中分布的情況,還可將空間格子分為原始格子、底心格子、體心格子及面心格子四種可能的型式。這樣,在晶體中共有14種不同的空間格子型式,通常稱為14種布拉維空間格子,也稱為14種平移格子或移動格子。
| 原始格子(P) | 底心格子(C) | 體心格子(I) | 面心格子(F) |
| | C=P | I=P | F=P |
| | | I=C | F=C |
| | | | |
| | C=P | | F=I |
| | 與本晶系對稱不符 | I=R | F=R |
| | 不符合六方對稱 | 與空間格子的條件不符 | 與空間格子的條件不符 |
| | 與本晶系對稱不符 | | |
註:六方底心格子即六方原始格子。
綜合考慮平行六面體的形狀和結點分布,空間格子共有14種。它最初是由布拉維推導出來的,故又稱為14種布拉維空間格子(表1)。
既然平行六面體有7種形狀和4種結點分布方式,那么,空間格子為什麼不是28種而是14種呢?這是因為某些格子類型是重複的,還有些格子類型與所在晶系的對稱不符,因而不能出現在該晶系中。
例如,三斜面心格子可以重新劃分為三斜原始格子;四方底心格子可以轉變為四方原始格子;單斜體心格子可以轉變為單斜底心格子等。在等軸晶系中,不存在立方底心格子,因為與本晶系對稱不符。
三斜面心格子可以重新劃分為三斜原始格子  | 四方底心格子可以轉變為四方原始格子  | 單斜體心格子可以轉變為單斜底心格子  |
單位平行六面體
眾所周知,晶體構造就是
單位平行六面體在三維空間做無間隙的堆疊或穿插組合。顯然,確定這種能代表空間格子類型的最小結構基元具有重要的意義,在研究格子構造中,這種單位平行六面體的劃分要求遵循下列原則:
① 所選的單位平行六面體應能反映整個結點分布所具有的對稱性;
② 所選的單位平行六面體棱間的直角最多;
③ 所選的單位平行六面體體積最小。
 圖1 單位平行六面體的選擇
圖1 單位平行六面體的選擇圖1是具有
對稱的點陣,圖中標出了6種選擇方式。顯然方式3、4、5、6的四種劃分都與
的對稱不符,在剩下的方式1、2中,都滿足選取原則①、②,但方式1的體積最小,滿足選取原則③,故應選取方式1作為
點陣的單位平行六面體。
描述單位平行六面體一般有6個參數,即3根棱長a、b、c及其間的夾角
,稱為單位平行六面體的晶格常數。
各晶系單位平行六面體及附加結點格子
按照上述單位平行六面體的劃分,對7個晶系的晶體進行分析,得到了如下7個晶系單位平行六面體的晶格常數特徵,相應各晶系單位平行六面體的基本幾何形狀見表2。
 (a)立方格子 |  (b)四方格子 |  (c)六方格子 |
 (d)三方格子 |  (e)斜方格子 |  (f)單斜格子 (f)單斜格子 (g)三斜格子 (g)三斜格子 |
顯然,單位平行六面體品格常數與晶體外形研究中給出的晶體幾何常數是完全一致的,這也說明了晶體內部的點陣構造決定了晶體的外形特徵。
對上面的單位平行六面體進行附加結點的分析,按分布方式不同可劃分出附加結點格子的基本類型,見表3。
底心格子:結點分布在平行六面體的8個角頂和1對平面的中心,又可細分為:
C心格子(C):結點分布在單位平行六面體的8個角頂和平行於(001)的1對平面的中心。
A心格子(A):結點分布在單位平行六面體的8個角頂和平行於(100)的1對平面的中心。
B心格子(B):結點分布在單位平行六面體的8個角頂和平行於(010)的1對面的中心。
一般情況下,底心格子即C心格子。對A心或B心格子,可以轉換為C心格子時,應儘可能予以轉換。僅在特殊情況下可直接使用A心或B心格子而無需轉換。
體心格子(I):結點分布在平行六面體的8個角頂和體心。
面心格子(F):結點分布在單位平行六面體的8個角頂和每一個面的中心。
原始格子  | 底心格子:C心格子  | 底心格子:A心格子  |
底心格子:B心格子  | 體心格子  | 面心格子  |

















 圖1 單位平行六面體的選擇
圖1 單位平行六面體的選擇








 (f)單斜格子
(f)單斜格子 (g)三斜格子
(g)三斜格子