用於分析一類可壓縮流動的一種近似理論。
基本介紹
- 中文名:空氣動力學小擾動理論
- 外文名:small-perturbation theory of aerodynamics
- :
- :
簡介
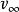

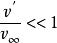

小擾動方程
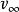


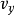

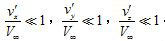

亞聲速和超聲速流動情形

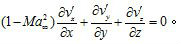
跨聲速流動情形
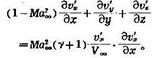
高超聲速流動情形
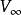
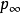


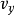



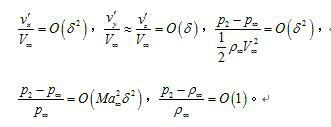
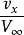

用於分析一類可壓縮流動的一種近似理論。
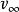

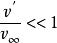

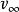


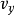

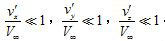


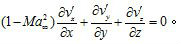
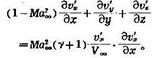
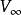
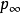


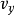



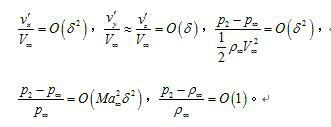
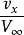

空氣動力學小擾動理論簡介 用於分析一類可壓縮流動的一種近似理論。當無窮遠處勻直氣流以小攻角流過扁平或細長物體時,物體給該氣流的擾動一般較小。如原勻直流的...
空氣動力學(上冊)由清華大學出版社出版,作者是吳子牛主編 王兵,周睿,徐珊姝編著...... 第3章 高速空氣動力學3.1 可壓縮流動與一維定常流動理論3.2 高速流動的小...
書名:空氣動力學基礎 作者: 陳浮,權曉波,宋彥萍 責編:劉瑤 I S B N:978-...7.3.2小擾動理論的高超聲速相似律7.4高超聲速流動的牛頓流模型及其修正...
空氣動力學是力學的一個分支,研究飛行器或其他物體在同空氣或其他氣體作相對運動...研究這類流動的主要理論和近似方法有小擾動線化方法,普朗特-格勞厄脫法則、卡門...
通常所說的空氣動力學研究內容是飛機,飛彈等飛行器在各種飛行條件下流場中氣體的...主要的理論處理方法有超聲速小擾動理論、特徵線法和高速邊界層理論等。跨聲速無...
這些超聲速流的線化理論圓滿地解決了流動中小擾動的影響問題。空氣動力學歷史實驗研究 編輯 空氣動力學發展的另一個重要方面是實驗研究,包括風洞等各種實驗設備的...
動力學問題,特別是對與氣動彈性動力學分析密切相關的機翼非定常空氣動力計算理論...4.1.5小擾動理論4.1.6經典聲學的簡化4.1.7邊界條件4.1.8對稱和反對稱...
空氣動力學是力學的一個分支,研究飛行器或其他物體在同空氣或其他氣體作相對運動...這些超聲速流的線化理論圓滿地解決了流動中小擾動的影響問題。在飛行速度或流動...
3.1.8一維定常流動理論1973.2高速流動的小擾動理論2103.2.1理想等熵定常...本書分為上、下兩冊,涉及空氣動力學的經典內容和一些非經典內容。經典內容包括...
三維流動的方程更複雜,但當合速大於聲速時,方程仍是雙曲型的,在小擾動的假設下(見空氣動力學小擾動理論),以速度勢表示的流動方程可線性化為:式中Ma∞為來流...
高超聲速流動的理論研究, 始於20世紀40年代後期中國學者錢學森和郭永懷對高超聲速相似律(見空氣動力學小擾動理論)的研究。60年代中期是高超聲速流動無粘近似理論蓬勃...
定常無粘性跨聲速位勢流,在小擾動的條件下可得到簡化的但仍為非線性的小擾動方程和相應的邊界條件(見空氣動力學小擾動理論)。從方程和邊界條件中可以看出,對於兩...
