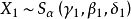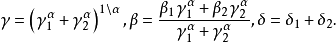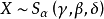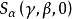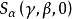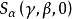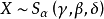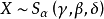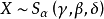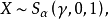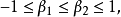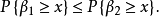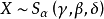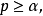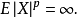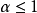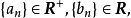穩定分布的定義
穩定分布有多種等價的定義方式,這裡根據
穩定性(Stability Property)、
吸引域(Domain of Attraction)和
特徵函式(Characteristic Function)給出
穩定分布的三種定義。
穩定性定義
如果對於任意正數A和B,存在正數C和一個實數D∈R,使得
成立,則稱隨機變數X是一個穩定分布。其中,隨機變數
和
是
的獨立樣本:符號“
”表示分布相同。如果X和-X具有相同的分布,則稱穩定隨機變數
為對稱穩定的。如果當D=0時式(1)仍成立,則稱
為嚴格穩定的。
此定義表明,
穩定隨機變數的加法是封閉的,而且其機率密度函式的卷積也是封閉的。若
是相互獨立的穩定隨機變數,並且具有相同的
參數,則其線性組合
也服從穩定分布,並且具有相同的
參數。
定理1 如果對任意穩定隨機變數X,總均存在數
使得C滿足
則
稱為
穩定變數,其中
稱為特徵指數(Characteristic Exponent)或穩定係數(Indexof Stability)。
吸引域定義
如果隨機變數
存在一個吸收域,即存在一個
獨立同分布的隨機變數序列
以及序列
使得
則稱隨機變數X是一個穩定分布。此定義也稱廣義中心極限定理,其中“
”表示依分布收斂。特別地,如果
滿足獨立同分布且具有有限
方差,則高斯分布是其極限分布,式(3)便成為
中心極限定理的原始表述。
特徵函式定義
穩定分布並不存在統一、封閉的機率密度函式(Probability Density Functions,PDF)解析表達式,但它存在統一的特徵函式(Characteristic Function,CF)。特徵函式是表示
穩定分布最方便的方法,若隨機變數X服從穩定分布規律,若且唯若其特徵函式滿足
式中:
為符號函式。可見,
穩定分布的特徵函式完全由4個參數
唯一確定。符合特徵函式式(4)的4個參數稱為標準參數系S,並記為
。
(1)
稱為特徵指數(Characteristic Exponent),它決定了穩定分布的機率密度函式拖尾厚度。它的值越小,分布的拖尾也就越厚,所以分布的衝擊性越強,即偏離中值的樣本個數越多:隨著
值的不斷增大,分布的拖尾將變淺,衝擊強度降低,如圖1和圖2所示。特別說明,
穩定分布當
=2時退化為
高斯(Gauss)分布,當
=1並且
時為
柯西(Cauchy)分布,為此我們定義0<
<2為分數低階
穩定分布,以區別於
=2的高斯分布。
(2) γ為尺度參數(Scale parameter)或
分散係數(Dispersion),它是關於分布樣本偏離其均值的一種度量,其意義類似於高斯分布時的方差。實際上,在高斯分布情況下γ為方差的兩倍。
(3) β為偏斜參數(Skewness parameter),它決定了分布的對稱程度。當β=0時,該分布是對稱的,通常稱為對稱α穩定(Symmetric α-Stable,SaS)分布。高斯分布和柯西分布都屬於對稱α穩定分布,β>0和好β<0分別對應分布的左偏和右偏。
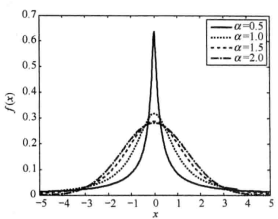 圖1標準對稱α穩定分布的機率密度函式
圖1標準對稱α穩定分布的機率密度函式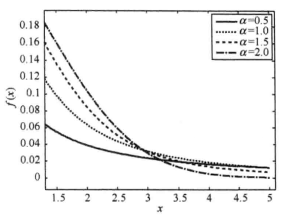 圖2α穩定機率密度函式的拖尾特性
圖2α穩定機率密度函式的拖尾特性(4) δ為位置參數(Location parameter)。考慮到特徵函式與其機率密度函式互為傅立葉變換,所以式4中的指數項
表征了機率密度函式在X軸的偏移。對於
分布而言,δ表示分布的均值1<α≤2或中值0<α≤1。當γ=1且δ=0時,則α穩定分布稱為標準
穩定分布。
穩定分布的性質
性質1
性質2
性質3
對於任意0<α<2,有
。對於β>0,稱
是左偏斜的:對於
β<0,稱
是右偏斜的。當β=1和β=-1時,
分別對應完全左偏斜和完全右偏斜。
性質4
若且唯若β=0時,
關於δ對稱的:若且唯若β=0且δ=0時,
關於0對稱。
性質5
若
,並且
那么存在兩個獨立同分布的隨機變數
,具有分布
使下式成立,即
性質6
性質7
這表明:當
時,分數低階
穩定隨機變肇沒有有限的二階矩,許多在高斯情況下有效的技術不能套用於這種場合,例如譜分析和最小二乘方法等;當
時,甚至沒有有限的—階矩,從而使數學期望的使用也受到影響。分數低階統計量是用來研究
穩定分布的有力工具。
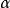
















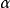

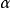






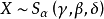









 圖1標準對稱α穩定分布的機率密度函式
圖1標準對稱α穩定分布的機率密度函式 圖2α穩定機率密度函式的拖尾特性
圖2α穩定機率密度函式的拖尾特性