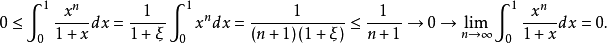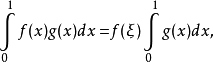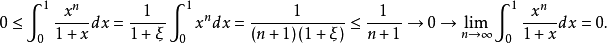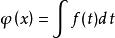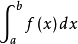基本介紹
定理,推導,套用,1.定理的直接套用,2.積分第二中值定理在證明不等式中的套用,3.積分中值定理在極限中的套用,
定理
設f(x)在[a,b]上可積,g(x)在[a,b]上單調,則存在ξ∈[a,b],使得
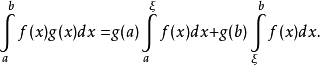
推導
首先需要證明,若函式f(x)在[a,b]內可積分,則Φ(x)在此區間內為一連續函式。
證明:設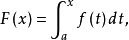 則
則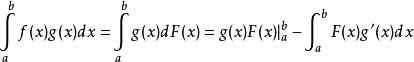
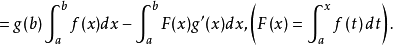
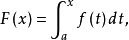
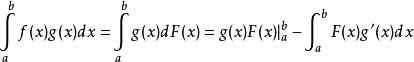
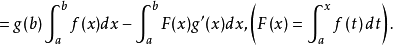
因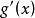 在[a,b]上不變號,則由積分第一中值定理知,在[a,b]上至少存在一點ξ,使得
在[a,b]上不變號,則由積分第一中值定理知,在[a,b]上至少存在一點ξ,使得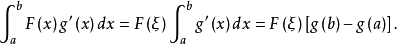
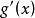
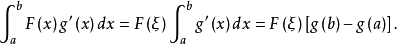
於是,有
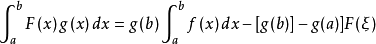
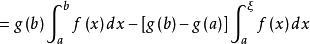
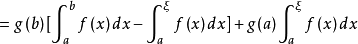
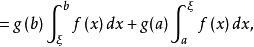
即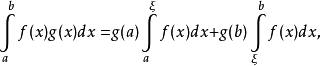 得證。
得證。
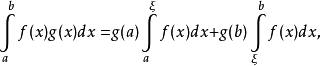
套用
在一些比較複雜的極限證明過程中套用積分第二中值定理可以得到很好的結果,而且計算過程簡單易懂,證明方式也很多,下面給出它在各個方面的重要套用。
1.定理的直接套用
例1.設f(x)在[a,b]上可積,g(x)在[a,b]上單調遞增且非負,在a,b處連續,那么在[a,b]上存在ξ,使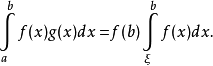
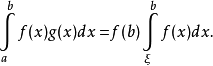
證 明 :令x=b-t,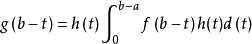 ,因為h(t)非負且單調遞減( 0<t<b-a)利用公式有
,因為h(t)非負且單調遞減( 0<t<b-a)利用公式有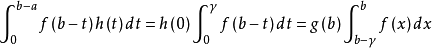
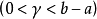 ,而a<ξ <b-
,而a<ξ <b-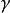 ,即
,即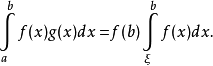
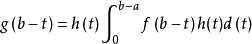
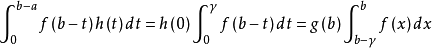
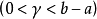
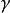
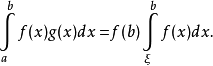
2.積分第二中值定理在證明不等式中的套用
例2.證明x>0時,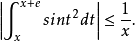
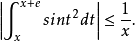
證明:取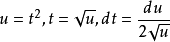 ,由積分中值定理和它的推論可得:
,由積分中值定理和它的推論可得:
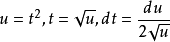
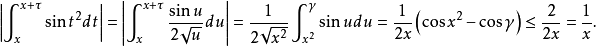
3.積分中值定理在極限中的套用
例3.證明極限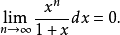
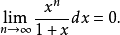
證明:由積分中值定理和它的推論可得:令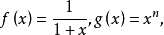
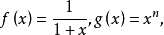
令可知g(x)在[0,1]上連續,而且不變號。所以存在ξ使得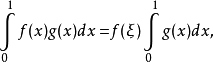 因此有以下式子
因此有以下式子