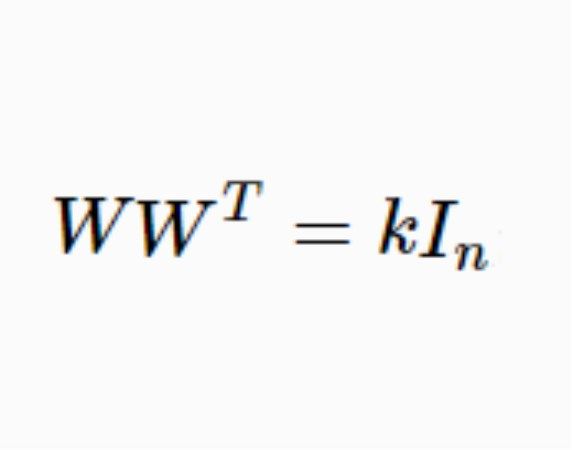稱重矩陣

稱重矩陣(weighing matrix)是阿達馬矩陣的推廣，若W是元素為0，±1的n階矩陣，且使WW=kI_n，則稱W為n階稱重矩陣，k=n的稱重矩陣就是n階阿達馬矩陣，k=n-1的對稱稱重矩陣就是n階對稱C矩陣，人們猜測：對每個正整數t及每個k=0，1，…，4t，存在4t階稱重矩陣，當k=4t時，這就是阿達馬矩陣猜測，若將v階稱重矩陣中的-1換作1，得到的是某個(v，k，λ)-SBIBD的關聯矩陣，則稱這樣的稱重矩陣為平衡稱重矩陣，這類矩陣的討論有助於發現新的BIBD設計。

基本介紹

• 中文名：稱重矩陣
• 外文名：weighing matrix
• 所屬學科：數學
• 所屬問題：組合學（組合設計理論）
• 簡介：阿達馬矩陣的推廣

基本介紹

定義 設W為-矩陣，若

則稱W為一個重量(weight)k的n階稱重矩陣(weighing matrix)。記作。k=n時的稱重矩陣便是n階H-陣。

【例1】設

則彬，即W為一個。

相關結論

引理1 (Craigen)若4m階與4n階H-陣都存在，則存在4mn階(1，-1)-矩陣S與R滿足下述條件：

(i)， （2）

(ii)。 （3）

證明設H為4m階H-陣，K為4n階H-陣，將它們表為如下形狀：

其中諸H_i為m×4m矩陣，諸K_i為n×4n矩陣，令

則R與S都是(1,-1)-矩陣。由於i≠j時。故由引理1得

即得引理。

引理2 若4m階與4n階H-都存在，則存在一對不相交的W(4mn,2mn)。

證明設H為4m階H-陣，K為4n階H-陣，R與S分別由式(5)與式(6)給出，令

於是由式(2)與式(3)得

即X與Y為一對。又因R與S都是-矩陣。故X與Y必不相交。