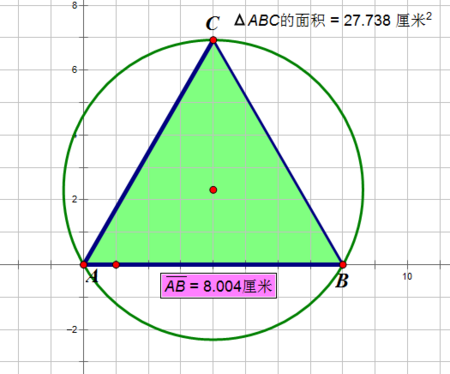
秦氏定理,用於三角面積周長題目的快速解題。
基本介紹
- 中文名:秦氏定理
- 外文名:QinshiTheorem
- 別名:三角快速解題定理
- 提出者:秦天琦
- 提出時間:2016年
- 適用領域:三角題目
- 套用學科:數學
定律,適用範圍,定律影響,
定律
在三角形中已知一角與其對邊。求其最大面積或最大周長。最大面積公式=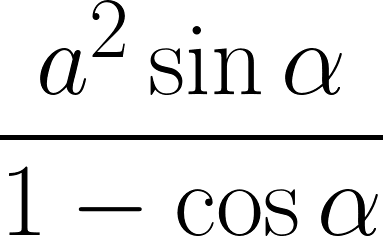
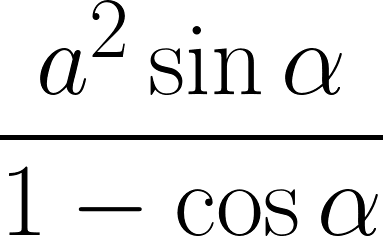
公式
最大面積與最大周長都在三角形為等腰時最大
在圓中畫出三角形

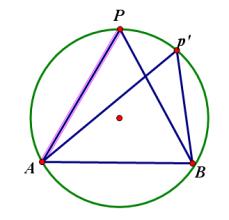
在圓中畫出三角形
∠p在圓上運動不改變大小,AB為定邊,易知當p點過垂直於AB的直徑時三角形PAB面積最大,即PA=PB。由余弦定理知



公式
適用範圍
三角知一角一對邊的面積問題的快速解法
已知 3
1
, 由此可以得到哪些結論? 這樣的試題便是開放型試題。
開放型題目的引入,可以引導學生從不同角度來思考,不僅僅思考條件本身,而且要思考條件之間的關係。要根據條件運用各種綜合變換手段來處理信息、探索結論,有利於思維起點靈活性的培養,也有利於孜孜不倦的鑽研精神和創造力的培養。
二、以思維靈活性的提高帶動思維其他品質的提高,以思維其他品質的培養來促進思維靈活性的培養
由於思維的各種品質是彼此聯繫、密不可分的,處於有機的統一體中,所以,思維其他品質的培養能有力地促進思維靈活性的提高,下面就思維品質中一些性質談點感悟。
(1)思維的深刻性指思維過程的抽象程度,指是否善於從事物的現象中發現本質,是否善於從事物之間的關係和聯繫中揭示規律。
例:方程sinx=lgx的解有( )個。
(A)1 (B)2 (C)3 (D)4
學生習慣於通過解方程求解,而此方程無法求解常令學生手足無措。若能運用靈活的思維換一
個角度思考:此題的本質為求方程組 的公共解。運用數
定律影響
大大加快解題速度