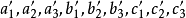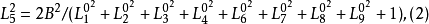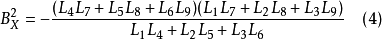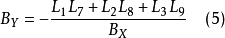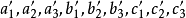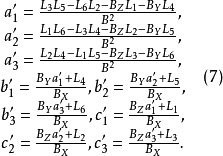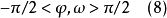相對定向

相對定向（relative orientation）是指恢復或確定象對在攝影時的相對關係，即解算立體像對相對方位元素的工作，恢復兩光束間相對方位的工作，理論依據是同名光線共面的原則。相對位置的表示方法有兩種：（1）單獨象對相對定向；（2）連續象對相對定向。解求的方法有兩種：（1）光學機械法；（2）解析法。

基本介紹

• 中文名：相對定向
• 外文名：relative orientation
• 概念：確定象對在攝影時的相對關係
• 表示方法：單獨或連續像對相對定向
• 解求方法：光學機械法和解析法
• 學科：測繪科學

簡介

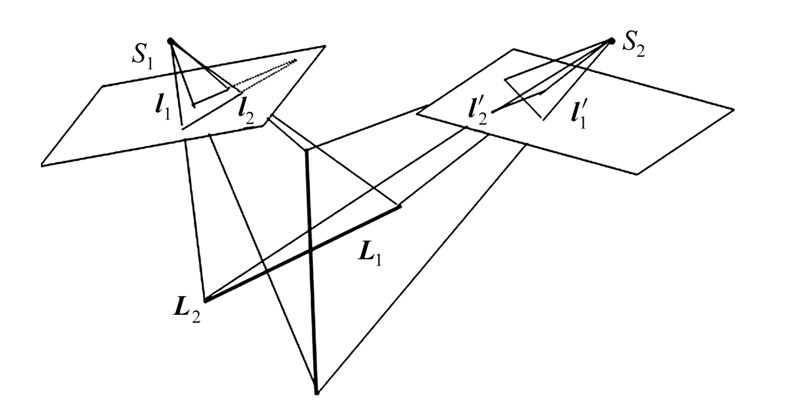
相對定向是指恢復或確定象對在攝影時的相對關係，理論依據是同名光線共面的原則。相對位置的表示方法有兩種：（1）以攝影基線為基準，用象對兩個光線束的五個角旋轉值表示，稱為單獨象對相對定向；（2）以其中一張相片為基準，另一張相片的兩個直線移動值和三個角旋轉值表示，稱為“連續象對相對定向”。解求的方法有兩種：（1）光學機械法。在立體測圖儀上利用投影器的角旋轉和基線支架的直線運動，消除象對內至少五個同名象點的上下視差；（2）解析法，在坐標量測儀上量測象對中至少五個同名點的坐標，根據相對定向元素與上下視差的關係解算相對定向元素值。完成象對的相對定向，即可以認為已獲得自由比例尺和處於空間任意位置的攝區的幾何模型，此時的模型可能是傾斜的。

相對定向元素

確定一個像對的兩種像片相對位置關係所需要的元素叫做相對定向元素。它是描述立體像對中兩張像片的相對位置和姿態關係的元素。一個像對的相對定向元素共有5個，這5個相對定向元素隨著所選取的像空間輔助坐標系的不同，通常有兩種不同的表達形式。

連續像對的相對定向元素

欲恢復一個像對兩張像片之間的相關位置，可以以像對的左片為基準，只通過確定右片相對於左片的5個元素(b_y，b_z，α_x，ω，k)來實現。由於這種相對定向元素能連續地恢復相鄰或一條航線上所有投影光束之間的相對方位，故這種相對定向元素被稱為連續像對的相對定向元素。其中，b_y、b_z為攝影基線在像空間輔助坐標系中Y、Z坐標軸上的投影，稱為攝影基線的兩個分量；α_x為右像片主光軸S₂O₂在X₂Z₂坐標面上的投影與Z₂軸的夾角；ω為右像片主光軸S₂O₂與X₂Z₂坐標面之間的夾角；k為Y₂軸在右像片平面上的投影與右像片像平面坐標系y₂軸之間的夾角。

單獨像對的相對定向元素

欲恢復一個像對兩張像片的相關位置，還可以選擇攝影基線B為像空間輔助坐標系的X軸，通過確定左、右片的5個元素(α_x1，k₁，ω₂，α_x2，k₂)來實現。由於採用這種相對定向元素來確定一個像對的兩種像片相對位置時，左、右光束需要分別移動才能實現，這種相對定向元素考慮建起一個像對的立體幾何模型(即稱單模型或獨立模型)，而不顧及相鄰模型間的連續性，故這種相對定向元素稱為單獨像對的相對定向元素。其中，ω₂為左、右兩像片主核面之間的夾角，由左核面起算，逆時針為正，順時針為負；α_x1、α_x2為左、右主核面上左、右主光軸與攝影基線垂線之間的夾角，由垂線起算，順時針為正，逆時針為輔；k₁、k₂為左、右主核線與左、右像平面坐標系x軸間的夾角，由主核線起算，逆時針至x軸正方向為正。

相對定向直接解的數學模型

數學模型的元素

若數字影像對的同名點在左右像平面坐標系中的坐標為(x,y)，(x',y')，左右兩架數位照相機拍攝時的焦距分別為f，f'，數字影像對的拍攝基線長為B，拍攝極限的三個分量為B_X，B_Y，B_Z，拍攝時像空間旋轉矩陣的變換係數為，其中基線長、旋轉矩陣係數都是相對定向的元素。

相對定向直接解的基本數學模型

數位照相機的相對定向直接解的基本數學模型為

式中。

根據相對定向直接解的基本數學模型，不需要任何基本近似值就能直接解得8個係數和焦距f，f'。其解法是通過同名點匹配，即左右相對匹配10對同名點，根據10對同名點的像平面坐標值，建立10個方程組，求解方程組獲得。

相對定向元素的解算

數字影像對拍攝基線分量的計算

利用（1）式求得係數，f和f'，根據立體像對三角元素旋轉矩陣的特性和基線長B與其分量B_X，B_Y，B_Z的數學關係，經數學變形後得到

由

可以求得，則

由（4）式可得B_X的正負兩個值，由於右相片的攝影中心S'始終在攝影測量坐標系的正方形，故取B_X≥0的值。求得B_X後，由數字攝影測量學原理可得

求解數字影像對選擇矩陣的元素

由（2）和（3）求得，由（4）~（6）求得B_X，B_Y，B_Z後，再根據數字影像對旋轉矩陣是正交矩陣的特性，疊代求解矩陣係數，其計算式為

由（2）式可知，L₅可取“+”號，也可取“-”號。L₅取不同的符號，會使旋轉矩陣元素產生兩組不同的解，而每個像對的相對定向矩陣是惟一的。

數字影像對方法元素的確定

為了確保右像片與左像片構成立體像對，右像片的方位元素φ，ω必須滿足（8）式。由此式就可以確定相對定向的一個正確解，即

右像片攝影方向元素（φ，ω）可按下面方法確定。由（7）式解算出右像片三角元素旋轉矩陣的9個元素後，再根據解析空中三角測量中計算角元素的嚴密公式

求解角元素φ，ω，k，確定旋轉矩陣和L₅的值。