“角度前方交會”是通過觀測角A和角B求出點P坐標的定位方法;“方位角前方交會”是通過觀測方位角AP和BP求出點P坐標的定位方法。
基本介紹
- 中文名:前方交會
- 外文名:Intersection ahead
- 描述:觀測角A和角B求出點P坐標
- 套用:定位方法
- 學科:測繪
定義

角度前方交會
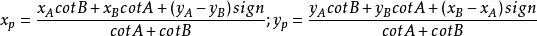
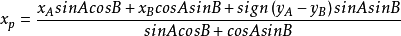
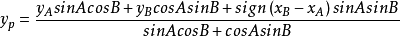
方位角前方交會


定位精度
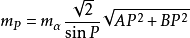

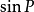
前方交會法
基於前方交會的5點相對定向
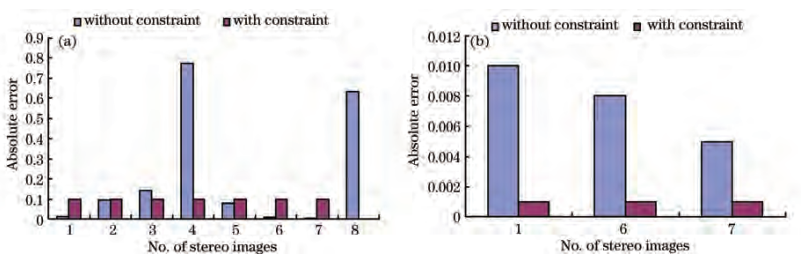 圖2(a)所有像對絕對誤差對比圖;(b)成功像對絕對誤差對比圖
圖2(a)所有像對絕對誤差對比圖;(b)成功像對絕對誤差對比圖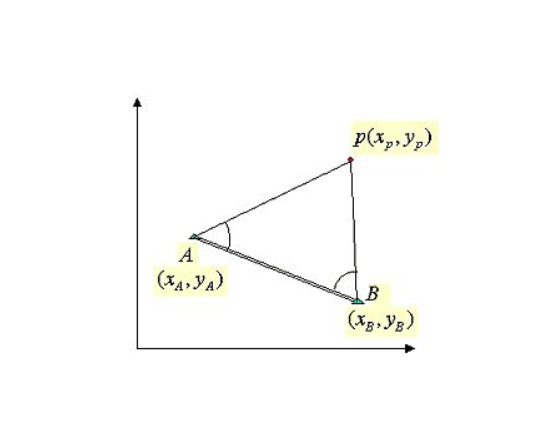
“角度前方交會”是通過觀測角A和角B求出點P坐標的定位方法;“方位角前方交會”是通過觀測方位角AP和BP求出點P坐標的定位方法。

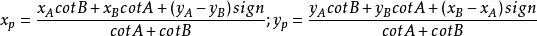
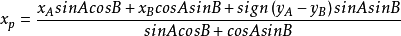
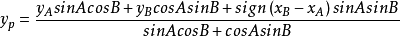


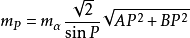

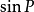
 圖2(a)所有像對絕對誤差對比圖;(b)成功像對絕對誤差對比圖
圖2(a)所有像對絕對誤差對比圖;(b)成功像對絕對誤差對比圖“角度前方交會”是通過觀測角A和角B求出點P坐標的定位方法;“方位角前方交會”是通過觀測方位角AP和BP求出點P坐標的定位方法。...
空間前方交會,是指恢復立體像對攝影時的光束和建立幾何模型後,利用同名光線的交會確定模型點空間位置的方法。...
是一種經常採用的加密控制點的方法。常用的幾種方法有:前方交會、側方交會、後方交會。...
前方交會法是指如果已知A、B兩點的坐標,為了計算未知點P的坐標,只要觀測∠A和∠B即可。這種測定未知點P的平面坐標的方法。...
角度交會法是指從兩個(或三個)已知點測定已知方向與待定點方向之間的水平夾角,以交會出待定點位置的方法。...
前方交會角差圖解法(forward graphic inter-section method with angular difference)快速而精確地放樣點位的一種方法.如圖,由控制點A,B和放樣點屍的坐標反算放樣...
側方交會法,是交會法測量的一種,類似於前方交會。交會角確定時,點位中誤差隨測角大小變化。...
根據坐標已知的點測定待定點平面位置的一種方法。在兩個(或兩個以上)已知點上對待定點觀測水平角的,稱為“前方交會法”;在待定點上對3個(或3個以上)已知點...
後方交會是指僅在待定點上設站,向三個已知控制點觀測兩個水平夾角a、b,從而計算待定點的坐標,稱為後方交會。交會測量是加密控制點常用的方法,它可以在數個已知...
交會點測量(intersection points survey)是指加密平面控制點的一種測量方法,又稱交會法測量或交會測量。交會點測量常用的方式有測角的前方交會,側方交會、後方交會和...
以兩個已知控制點為中心,分別以目標點與兩已知控制點的距離為半徑劃圓,交會點即為要求目標點(注意方向二選其中一個)。這種方法稱為距離交會法。在水平位移監測中...
交會測量(intersection survey)是根據多個已知點的平面坐標(或高程),通過測定已知點到某待定點的方向或(和)距離(或測定其豎直角),以推求此待定點平面坐標(或高程...
像對1、2和3的基高比大,可以認為其前方交會的結果最可靠,因此將其計算得到的地麵點坐標作為基準,分別計算像對1、像對2、像對3地麵點坐標在X,Y,Z3個方向上...
6.4 前方交會定點第7章 高程控制測量7.1 概述7.2 三、四等水準測量7.3 三角高程測量7.4 跨河水準測量第8章 全球定位系統8.1 概述...
