相對可構造性是由法國數學家、工程師萊維(Levy, A.)與休恩菲爾德((Shoenfield,J. R.)在美籍奧地利數學家哥德爾(Godel , K.)的可構造性方法的基礎上發展起來的一種可構造性理論。
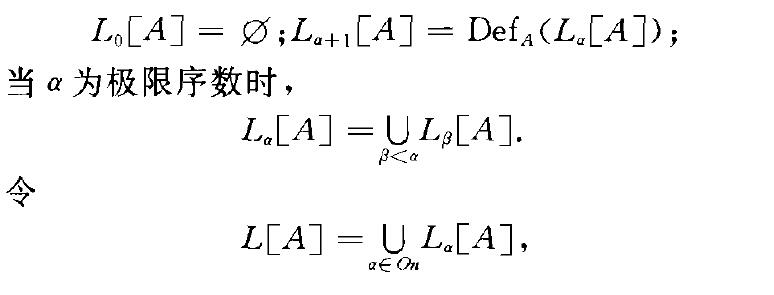
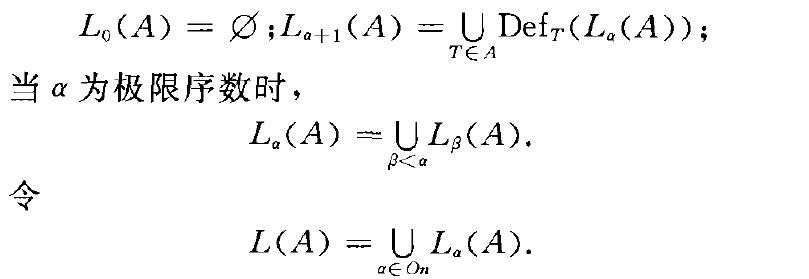
相對可構造性是由法國數學家、工程師萊維(Levy, A.)與休恩菲爾德((Shoenfield,J. R.)在美籍奧地利數學家哥德爾(Godel , K.)的可構造性方法的基礎上發展起來的一種可構造性理論。
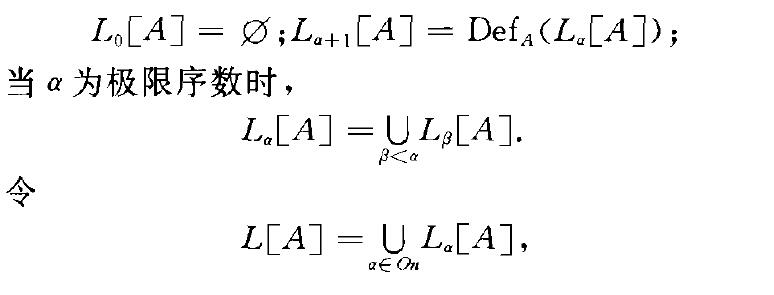
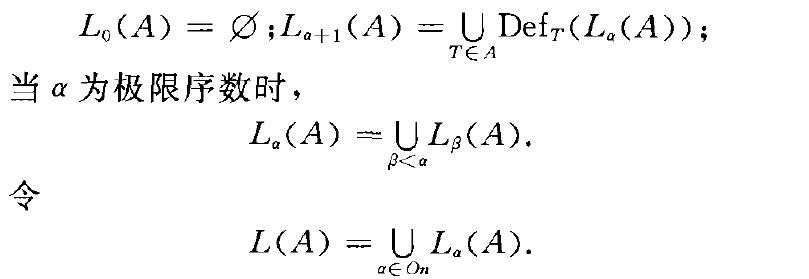
相對可構造性是由法國數學家、工程師萊維(Levy, A.)與休恩菲爾德((Shoenfield,J. R.)在美籍奧地利數學家哥德爾(Godel , K.)的可構造性方法的基礎上發展起來...
可構造性(constructibility)一種可構造集理論,是研究集合的可構造性以及可構造集合的各種特殊性質的理論,也是證明集合論命題相對相容性的一種重要方法。...
可構造性公理(axiom of constructibility)是集合論的一條重要公理,該公理斷言:所有集合都是可構造的。哥德爾(K.Gödel)為了證明連續統假設與ZFC是相容的,在1939...
可構造性因素指投資環境中,可以通過人的主觀努力,可以構造和改變的投資條件。如經濟體制、政治體制、教育體制、科技體制、政策、法令等。...
構造性數學是構造性地(即從某些初始對象出發,通過明確規定的操作)展開的數學理論的通稱。同建立在公理之上的數學相反,主要由於後者在刻畫自然數、實數等方面缺乏...
例如某一地質體的構造總體上是不均勻的,但可以把它統計性地劃分為一些相對均勻的區段,即可以把總體的非均勻變形看成是相鄰小區段均勻變形的結果。[1] ...
盤相對運動方式分為上盤相對下掉的正斷層、上盤相對上升的逆斷層與兩盤相對水平...按照構造形成的時間順序可將地質構造分為原生構造和次生構造。構造原生構造 ...
構造性成本模型最初發表於1981年巴里·勃姆《軟體工程經濟學》一書中,做為一種...COCOMO可以套用於三種不同的軟體項目:有機項目 - 相對較小、較簡單的軟體項目,...
構造繼承性(tectonic inheritance)是指新演化階段出現的構造格局,如洋、陸分布、...隨著地背斜的不斷褶皺隆起,逐漸發展成復背斜;而地向斜則仍相對坳陷,最後發展成...
構造性斷裂,多期次斷裂構造運動的疊加,使得斷裂帶內的地層、岩體遭受不同程度的...目前國內外重力重複測量還處於相對測量階段,即選定某一測點為原點,測量其他點...
非構造性證明是表述存在性的命題或定理的一種證明方式。...... 非構造性證明是“表述存在性的命題或定理”的一種證明方式:證明的過程中,不舉例而只證明語句是否正...
COCOMO,英文全稱為constructive cost model,中文為構造性成本模型。它是一種精確...進行項目開發,該項目與最近開發的其他項目有很多相似點,項目相對較小,而且並不...
按地震的成因可分數種,但最主要的是構造地震-即地殼運動(構造運動)造成岩石變形超出了岩石的承受能力,岩石斷裂並釋放能量形成振動。除此之外,都可以稱為非構造性...
礦石的構造形態及其相對可選性可以大致劃分如下:[2] 1.塊狀構造有用礦物集合體在礦石中占80%左右,呈無空洞的緻密狀,礦物捧列無方向性者,即為塊狀構造。其顆粒...
由於背斜岩層向上拱起,且油、氣的密度比水小,所以背斜常是良好的儲油、氣構造。與之相對,向斜是良好的儲水構造。背斜頂部受張力作用,岩性脆弱,易被侵蝕,在外力...
常形成構造岩帶。又分為兩類:脆性的扭性構造岩顯著特徵是大小不甚懸殊、磨蝕程度較高、礫石常具定向、成分相對複雜並可有較遠處的岩質混入;韌性構造岩,主要以...
;按其產生斷裂的作用力的性質可分為壓性斷裂、張性斷裂和扭性(或剪性)斷裂。...裂隙(節理):斷裂兩側的岩石僅因開裂而分離,並未發生明顯相對位移的斷裂構造;其...
塊狀構造,又稱“均一構造”。有多種地質體都可以塊狀構造這一術語進行描述,其共同點是物質排布的非定向與相對均一。...
利用地震台、網觀測資料和重複大地測量或短水準測量資料,可以確定活斷層的最新活動情況和相對位移量,預測其今後活動趨勢。地震基本烈度或地震危險性分析根據區域構造和...
地質構造運動地殼運動 編輯 地殼及組成物質岩石相對某一參照物發生 地質運動 的位置變化叫做地殼運動。固體地球堅硬的外層叫做地殼,地殼是由火山岩、沉積岩、變質岩和...
地表線性構造(surface lineament structure),是地球和其他星球的表面,常常有規模巨大、明顯和走向穩定的線性構造。它們可能是區域性的地形、地質構造或岩石類型的分界線...
dc是同伸展層序在零點(null point)之上的長度;Ri即擠壓運動或伸展運動的相對...的普遍性,並公認中國東部中生代以來經歷了由擠壓到拉伸的多次轉變;反轉構造的涵義...
剛性結構是在建築物或構造物上設定的一種耐震結構。相對柔性結構而言。其柱和梁的結構牢固,並設計有高強度的耐震壁,能增強建築物的整體剛性,承受強大地震力的衝擊...
結構性推理模是美國夏佩爾提出的普遍性科學推理模式之一。指在科學研究中通過現象的橫斷面結構探討對象的深層構造。認為科學發現是理性的,它可以有相對普遍的推理方式...
