盲目搜尋

盲目搜尋方法又叫非啟發式搜尋，是一種無信息搜尋，一般只適用於求解比較簡單的問題，盲目搜尋通常是按預定的搜尋策略進行搜尋，而不會考慮到問題本身的特性。常用的盲目搜尋有寬度優先搜尋和深度優先搜尋兩種。

基本介紹

• 中文名：盲目搜尋
• 別稱：非啟發式搜尋
• 類別：寬度優先搜尋、深度優先搜尋等

寬度優先搜尋

寬度優先搜尋又稱廣度優先搜尋。其基本思想是：從初始節點S₀開始進行節點擴展，考察S₀的第1個子節點是否為目標節點，若不是目標節點，則對該節點進行擴展；再考察S₀的第2個子節點是否為目標節點，若不是目標節點，則對其進行擴展；對S₀的所有子節點全部考察並擴展以後，再分別對S₀的所有子節點的子節點進行考察並擴展，如此向下搜尋，直到發現目標狀態S_g為止。因此，寬度優先搜尋在對第n層的節點沒有全部考察並擴展之前，不對第n+1層的節點進行考察和擴展。

以九宮問題為例，對初始節點S₀進行擴展，有四種操作有效，產生四個子節點S₁、S₂、S₃、S₄。對節點S₁考察發現它不是目標節點，應對其擴展。節點S₁有三種有效操作，但其中空格右移得到的狀態是其父節點的狀態，因此此狀態無效，即S₁節點僅有2個子節點S₅、S₆；對節點S₂考察，同樣只能生成2個子節點S₇、S₈；依次類推，可產生如右圖的搜尋樹。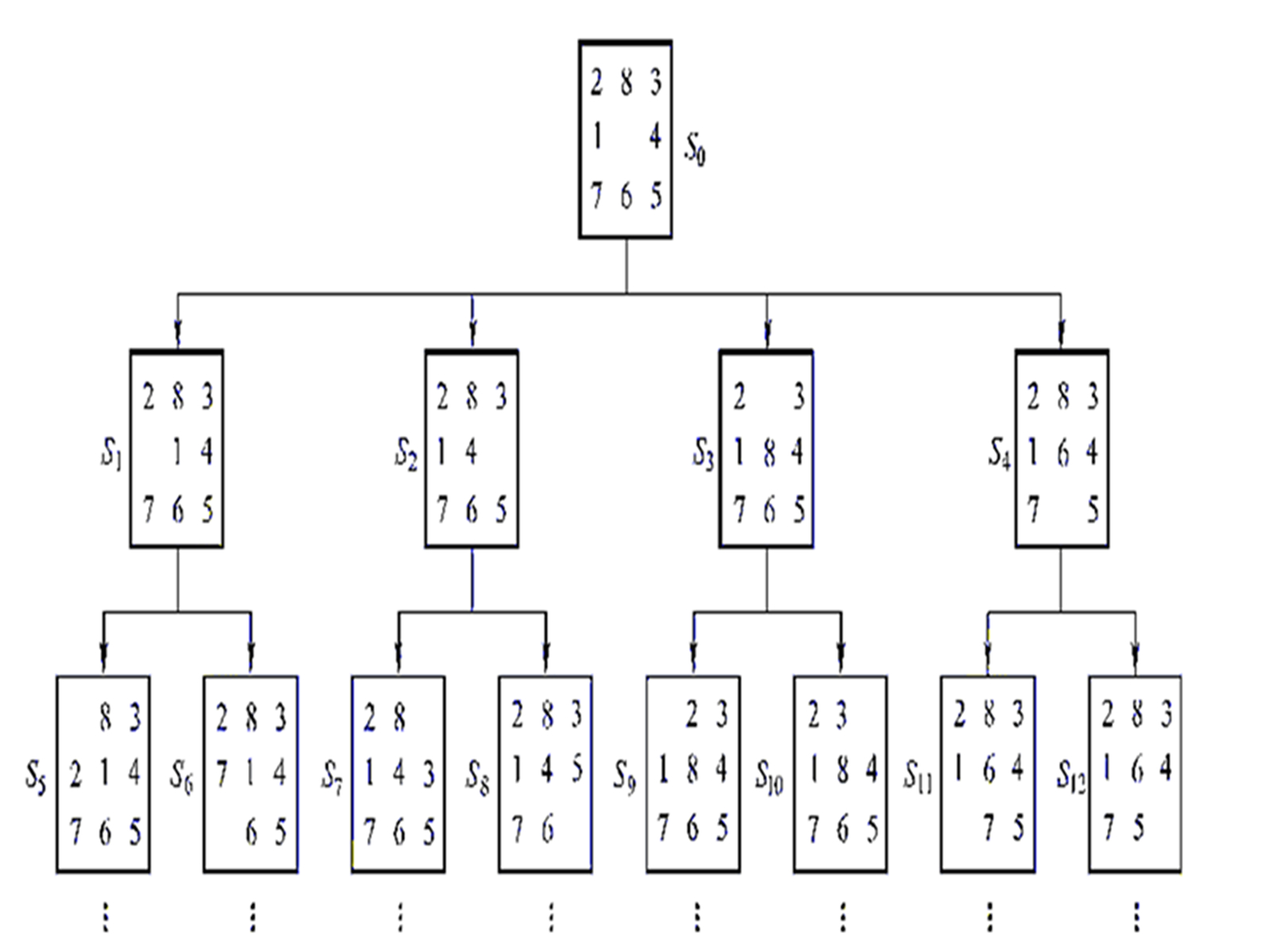

九宮問題的寬度搜尋法（深度為2）

寬度優先搜尋的盲目性較大，當目標節點離初始節點較遠時，將會產生許多無用節點，搜尋效率低，這是它的缺點。但是，只要問題有解，用寬度優先搜尋總可以得到解，而且得到的解是路徑最短的，這是它的優點。所以，寬度優先搜尋是完備的搜尋。

深度優先搜尋

深度優先搜尋的基本思想是：從初始節點S₀開始進行節點擴展，考察S₀擴展的最後1個子節點是否為目標節點，若不是目標節點，則對該節點進行擴展；然後再對其擴展節點中的最後1個子節點進行考察，若又不是目標節點，則對其進行擴展，一直如此向下擴展。當發現節點本身不能擴展時，對其1個兄弟節點進行擴展；如果所有的兄弟節點都不能夠擴展時，則尋找到它們的父節點，對父節點的兄弟節點進行擴展；依次類推，直到發現目標狀態S_g為止。因此，深度優先搜尋法存在搜尋和回溯交替出現的現象。

同樣，以九宮問題為例，對初始節點S₀進行擴展，有四種操作有效，產生S₁、S₂、S₃、S₄四個節點。先對節點S₄考察發現它不是目標節點，應對其進行擴展，但其中空格上移得到的狀態是其父節點的狀態，因此此狀態無效，即S₄節點僅有2個子節點S₅、S₆；對節點S₆進行考察發現不是目標節點，則進行擴展，得到S₆的子節點S₇；依次類推，可產生如右圖的搜尋樹。

九宮問題的深度搜尋法

在深度優先搜尋中，搜尋一旦進入某個分支，就將沿著該分支一直向下搜尋。如果目標節點恰好在此分支上，則可較快地得到問題解。但若目標節點不在該分支上，且該分支又是一個無窮分支，就不可能得到解。所以，深度優先搜尋是不完備的搜尋。

疊代加深搜尋

為克服深度優先搜尋陷入無窮分支死循環的問題，提出了有界深度優先搜尋方法。有界深度搜尋的基本思想是：預先設定搜尋深度的界限，當搜尋深度到達了深度界限而尚未出現目標節點時，就換一個分支進行搜尋。

在有界深度搜尋策略中，深度限制d是一個很重要的參數。當問題有解，且解的路徑長度小於或等於d時，則搜尋過程一定能找到解。但是，這不能保證最先找到的是最優解，此時深度搜尋是完備而非最優的。如d取得太小，解的路徑長度大於d，則在搜尋過程中就找不到解，此時搜尋過程不完備。但是，深度限制d不能太大，否則會產生過多的無用節點。為了解決深度限制d的設定，可以採用這樣的方法：先任意給定一個較小的深度限制，然後按有界深度搜尋，如在此深度找到解，則結束；否則，增大深度限制，繼續搜尋。此種搜尋方法稱為疊代加深搜尋。