皮特曼估計(Pitman estimate)是平方損失下位置參數的最優同變估計。亦稱最優同變估計。1939年由皮特曼(Pitman E.J.)建立,1951年經吉爾希克(Girshick M. A.) 和薩維奇 (Savage L. G.) 推廣的,位置參數的一種最優同變估計。
基本介紹
- 中文名:皮特曼估計
- 外文名:Pitman estimate
- 領域:數學
- 提出者:Pitman,E J.
- 提出時間:1939年
- 別名:最優同變估計
人物簡介,概念介紹,同變估計,
人物簡介
埃德溫·詹姆斯·喬治·皮特曼(Edwin James George Pitman)(1 9 9 7年10月29日至1993年7月21日)是澳大利亞數學家,對統計學和機率論作出了重大貢獻特別是,他被記住主要是由於他是皮特曼排列測試的創始人,皮特曼的接近度和皮特曼的效率。
皮特曼於1897年10月29日在墨爾本出生,並出席了墨爾本大學,居住在奧蒙德學院,畢業於一等榮譽。在1926年,他被任命為塔斯馬尼亞大學數學教授,直到他在1962年退休。
他是澳大利亞數學學會的創始成員和第二任校長。他也在澳大利亞統計學會內活躍,1978年他獲得了皮特曼獎章。
他自20世紀80年代由R.R.Rao,Pranab K. Sen等人廣泛研究了皮特曼對近似度或皮特曼近似度量指數機率分布的測度。
Pitman-Koopman-Darmois定理指出,只有指數族機率分布才能承認足夠的統計量,其維度隨樣本大小的增長而保持有界。
概念介紹
皮特曼估計,亦稱最優同變估計。1939年由皮特曼(Pitman E.J.)建立,1951年經吉爾希克(Girshick M. A.) 和薩維奇 (Savage L. G.) 推廣的,位置參數的一種最優同變估計。設總體X的機率密度函式形如f(x-θ),其中θ(-∞<θ<∞)是數值參數,EX2<∞;X1,…,Xn是來自X的隨機樣本,其聯合密度函式為f(x1-θ,…,xn-θ) 則估計量:
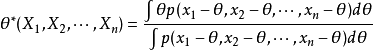
稱做θ的皮特曼估計。皮行曼估計是θ的無偏估計,其方差與θ無關,它在θ的一切無偏的同變估計中方差最小。
假設X1,…,Xn是簡單隨機樣本。對於移位指數總體X,假設其密度為:
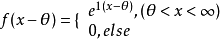
位置參數θ(-∞<θ<∞)的皮特曼估計為X(1)-1/n,其方差為1/n2;對於(θ-1/2,θ+1/2)上的均勻總體X,其密度為:

參數θ的皮特曼估計為 (X(1)+X(n))/2。
同變估計
不變估計(invariant estimate)亦稱同變估計,是評判估計量性能的準則之一在一些參數估計問題中,當樣本作某種特定變換時,可以要求估計量經受與之相應的一定變換。
在統計學中,不變估計的概念是可以用於比較相同數量的不同估計量的屬性的標準。 這是一種使估計師應該具有一定直觀吸引力的品質的想法的一種方式。 嚴格來說,“不變數”意味著當測量和參數以兼容的方式進行變換時,估計本身不變,但意義已經擴展到允許估計以適當的方式改變這種轉換。術語等值估計器用於形式數學上下文中,包括對估計器回響於數據集和參數化變化的變化方式的關係的精確描述:這對應於更一般數學中“等式”的使用。

