基本介紹
- 中文名:界面能
- 外文名:interfacial energy
- 定義:由原子排列畸變而升高的自由能
- 測量方式:界面張力平衡法等
- 實質:形核的阻力
簡介
界面能的各向異性
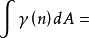
界面能的測量
界面張力平衡法




測量界面能的動力學方法
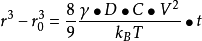
界面能的作用

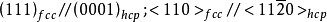


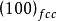

界面能對界面穩定性的影響
界面能對聚集形態的影響

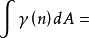




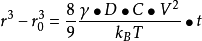

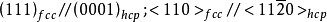


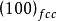


晶界上由於原子排列是畸變的,因而自由能升高,這額外的自由能稱為晶界能。小角度晶界的能量主要來自位錯能量(形成位錯的能量+將位錯排成有關組態所作的功)。而...
界面是指物質相與相的分界面。因為我們周圍的物質是以氣、液、固三種狀態存在,所以也就有了氣、液、固三相。在各相之間存在著氣-液、氣-固、液-液、液-固...
晶界上由於原子(離子)間結合鍵的變化及結構畸變,界面將存在著比體內高的剩餘能量,這就是界面能。晶界上兩個晶粒的質點排列取向有一定的差異,兩者都力圖使晶界上...
界面設計(即UI設計)是人與機器之間傳遞和交換信息的媒介,FaceUI稱包括硬體界面和軟體界面,是計算機科學與心理學、設計藝術學、認知科學和人機工程學的交叉研究領域。...
熱力學平衡時離子晶體的表面或界面由於有過剩的同號離子而帶有一種電荷,這種電荷正好被晶界鄰近的異號空間電荷層所抵消。這種現象就叫做界面特性。...
軟體界面(software interface)的定義並不十分統一。 狹義上說,軟體界面就是指軟體中面向操作者而專門設計的用於操作使用及反饋信息的指令部分。優秀的軟體界面有簡便...
兩相界面上,原子成一一對應的完全匹配,即界面上的原子同時處於兩相晶格的節點上,為相鄰兩晶體所共有,這種相界稱為共格界面。基於共格模型的計算使得人們能在原子...
人機界面(Human Machine Interaction,簡稱HMI),又稱用戶界面或使用者界面,是人與計算機之間傳遞、交換信息的媒介和對話接口,是計算機系統的重要組成部分。是系統和用戶...
設計界面是指為設計中所面對、所分析的一切信息互動的總和,它反映著人一物之間的關係。...
界面測試(簡稱UI測試),測試用戶界面的功能模組的布局是否合理、整體風格是否一致、各個控制項的放置位置是否符合客戶使用習慣,此外還要測試界面操作便捷性、導航簡單易懂...
晶體中相鄰疇區間的交接往往不是任意的,通常只有那些點陣匹配度較好,具有特定形態及結構,因而界面能較低的面缺陷能夠存在。人們通常按界面兩側晶體結構之間的關係將其...
(1)片狀滲碳體的表面積大,界面能高,球化退火時,將會自發球化。 (2)與滲碳體尖角接壤處的鐵素體碳濃度 Cα-k 大於與平面接壤處的碳濃度,在鐵素體內將引起...
式液晶顯示裝置,當接觸了螢幕上的圖形按鈕時,螢幕上的觸覺反饋系統可根據預先編程的程式驅動各種連結裝置,可用以取代機械式的按鈕面板,並藉由液晶顯示畫面製造出生動...
Windows 95的全新用戶界面給用戶以全新的感受。對於初學Windows 95的用戶,會體會到Windows 95啟動和其系統列上應用程式切換的簡便性;對於熟悉Windows 95的用戶,...
B/S架構,即瀏覽器和伺服器結構,用戶的工作界面可以通過www瀏覽器來實現,從適用範圍來講,B/S架構的ERP軟體不但適用於企業內部區域網路,也適用於外部的廣域網。即...
打開軟體界面,嗨格式PDF轉換器支持,PDF互轉Word,PDF互轉Excel,PDF互轉PPT,PDF轉圖片等。第三步:點擊【開始轉換】按鈕點擊“開始轉換”按鈕, 開始檔案格式轉換。...
Windows 1.0用戶界面(4張) Windows 1.0中滑鼠作用得到特別的重視,用戶可以通過點擊滑鼠完成大部分的操作。Windows 1.0 自帶了一些簡單的應用程式,包括日曆、記事...
新版系統重點強化了對觸摸操作的支持和最佳化,比如蜂窩形的主選單界面,不但看起來更美觀,而且比傳統方格式界面更易於觸摸點擊,另外各個命令圖示的位置都可以上下移動位...
